A Multiscale Model for Solute Diffusion in Hydrogels

Abstract

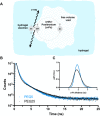
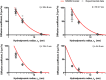
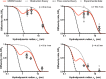
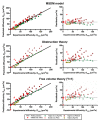
The number of biomedical applications of hydrogels is increasing rapidly on account of their unique physical, structural, and mechanical properties. The utility of hydrogels as drug delivery systems or tissue engineering scaffolds critically depends on the control of diffusion of solutes through the hydrogel matrix. Predicting or even modeling this diffusion is challenging due to the complex structure of hydrogels. Currently, the diffusivity of solutes in hydrogels is typically modeled by one of three main theories proceeding from distinct diffusion mechanisms: (i) hydrodynamic, (ii) free volume, and (iii) obstruction theory. Yet, a comprehensive predictive model is lacking. Thus, time and capital-intensive trial-and-error procedures are used to test the viability of hydrogel applications. In this work, we have developed a model for the diffusivity of solutes in hydrogels combining the three main theoretical frameworks, which we call the multiscale diffusion model (MSDM). We verified the MSDM by analyzing the diffusivity of dextran of different sizes in a series of poly(ethylene glycol) (PEG) hydrogels with distinct mesh sizes. We measured the subnanoscopic free volume by positron annihilation lifetime spectroscopy (PALS) to characterize the physical hierarchy of these materials. In addition, we performed a meta-analysis of literature data from previous studies on the diffusion of solutes in hydrogels. The model presented outperforms traditional models in predicting solute diffusivity in hydrogels and provides a practical approach to predicting the transport properties of solutes such as drugs through hydrogels used in many biomedical applications.

Figure 1

Scale effects in solute diffusion in hydrogels. The diffusion of a solute within a hydrogel occurs via aqueous solution and through liquid-filled, nano- to microscopic open spaces between the polymer fibers or free volume (dynamic, subnanoscopic, empty voids between the molecules). Which of these mechanisms dominates diffusion depends on the ratio between the hydrodynamic radius of the solute and the radius of the free volume voids in the hydrogel.

Figure 2

(A) In positron annihilation lifetime spectroscopy (PALS) experiments, positrons are implanted in the material. In the free volume voids, orthopositroniums (o-Ps) are formed. In larger free volume voids, the o-Ps will live for longer before annihilating with an electron from the void wall and decaying into two γ-rays. (B) Raw positron lifetime spectra obtained in two different samples, PEG5 and PEG25. (C) Probability density functions of the o-Ps in two different samples, PEG5 and PEG25, extracted by deconvoluting the positronium lifetime spectra.

Figure 3

Diffusivities predicted by the MSDM model compared against experimentally obtained diffusivities. Experimental diffusivities (gray circles; error bars denote mean ± s.d.; n = 10) and predicted diffusivities (solid red lines) are plotted against solute hydrodynamic radius (r_s) for PEG hydrogels with different mesh sizes (ξ).

Figure 4

Normalized diffusivities predicted by the MSDM model compared against experimentally obtained values. Experimental data (gray circles; error bars denote mean ± s.d.; n = 10) and theoretical predictions (lines) for the normalized diffusivity, D/D₀, versus solute hydrodynamic radius (r_s) for PEG hydrogels with different mesh sizes (ξ; mean ± s.d.; n = 4). The MSDM model (red solid line) predicts the existence and location of a local minimum and maximum in D/D₀, whereas free volume theory (black dashed line) and obstruction theory (black dotted line) do not. These local minima/maxima in D/D₀ are reflected in the experimental data.

Figure 5

Parity plot of predicted versus experimental diffusivity. The perfect prediction is illustrated as the 1–1 line plotted in black. The MSDM model (squares) by eq 6 predicts the experimental diffusivity of dextran solutes in both poly(ethylene glycol) hydrogels (PEG)^,, and alginate-based hydrogels^, more accurately than eqs 3 and 4—free volume theory (triangles) and obstruction theory (circles). Each color of data points represents a different study of the meta-analysis. In the residuals versus experimental diffusivity plot, the perfect prediction is shown as a black dotted line.

Figure 6

MSDM model accounts for different diffusion mechanisms depending on the scale of the solute. (A) When the solute size is comparable to the free volume pockets, the solute will diffuse though free volume. (B) When the solute is substantially larger than the free volume, it will diffuse with the liquid within the hydrogel and cross the mesh. (C) When the solute is larger than the mesh size, the diffusion will be hindered by the polymer fibers of the mesh.