Cyclic Changes in Active Site Polarization and Dynamics Drive the 'Ping-pong' Kinetics in NRH:Quinone Oxidoreductase 2: An Insight from QM/MM Simulations
- PMID: 31583178
- PMCID: PMC6776251
- DOI: 10.1021/acscatal.8b04193
Cyclic Changes in Active Site Polarization and Dynamics Drive the 'Ping-pong' Kinetics in NRH:Quinone Oxidoreductase 2: An Insight from QM/MM Simulations
Abstract
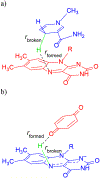
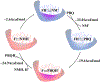
Quinone reductases belong to the family of flavin-dependent oxidoreductases. With the redox active cofactor, flavin adenine dinucleotide, quinone reductases are known to utilize a 'ping-pong' kinetic mechanism during catalysis in which a hydride is bounced back and forth between flavin and its two substrates. However, the continuation of this catalytic cycle requires product displacement steps, where the product of one redox half-cycle is displaced by the substrate of the next half-cycle. Using improved hybrid quantum mechanical/molecular mechanical simulations, both the catalytic hydride transfer and the product displacement reactions were studied in NRH:quinone oxidoreductase 2. Initially, the self-consistent charge-density functional tight binding theory was used to describe flavin ring and the substrate atoms, while embedded in the molecular mechanically-treated solvated active site. Then, for each step of the catalytic cycle, a further improvement of energetics was made using density functional theory-based corrections. The present study showcases an integrated interplay of solvation, protonation, and protein matrix-induced polarization as the driving force behind the thermodynamic wheel of the 'ping-pong' kinetics. Reported here is the first-principles model of the 'ping-pong' kinetics that portrays how cyclic changes in the active site polarization and dynamics govern the oscillatory hydride transfer and product displacement in this enzyme.
Keywords: Double displacement reactions; Kohn-Sham density functional theory; flavoenzyme; hydride transfer reactions; quantum mechanical/molecular mechanical calculations; quinone oxidoreductase 2; self-consistent charge density functional tight-binding theory; ‘ping-pong’ kinetics.
Figures






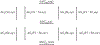
Similar articles
-
Interplay of flavin's redox states and protein dynamics: an insight from QM/MM simulations of dihydronicotinamide riboside quinone oxidoreductase 2.J Phys Chem B. 2011 Apr 7;115(13):3632-41. doi: 10.1021/jp1107922. Epub 2011 Mar 16. J Phys Chem B. 2011. PMID: 21410212 Free PMC article.
-
Theoretical determination of the redox potentials of NRH:quinone oxidoreductase 2 using quantum mechanical/molecular mechanical simulations.J Phys Chem B. 2009 Jun 11;113(23):8149-57. doi: 10.1021/jp901854a. J Phys Chem B. 2009. PMID: 19445526
-
A hydrogen bond network in the active site of Anabaena ferredoxin-NADP(+) reductase modulates its catalytic efficiency.Biochim Biophys Acta. 2014 Feb;1837(2):251-63. doi: 10.1016/j.bbabio.2013.10.010. Epub 2013 Nov 4. Biochim Biophys Acta. 2014. PMID: 24200908
-
Role of substrate dynamics in protein prenylation reactions.Acc Chem Res. 2015 Feb 17;48(2):439-48. doi: 10.1021/ar500321u. Epub 2014 Dec 24. Acc Chem Res. 2015. PMID: 25539152 Free PMC article. Review.
-
Amine oxidation by d-arginine dehydrogenase in Pseudomonas aeruginosa.Arch Biochem Biophys. 2017 Oct 15;632:192-201. doi: 10.1016/j.abb.2017.06.013. Epub 2017 Jun 15. Arch Biochem Biophys. 2017. PMID: 28625766 Review.
Cited by
-
Polymorphisms and Pharmacogenomics of NQO2: The Past and the Future.Genes (Basel). 2024 Jan 10;15(1):87. doi: 10.3390/genes15010087. Genes (Basel). 2024. PMID: 38254976 Free PMC article. Review.
-
Neuroprotective Properties of Quinone Reductase 2 Inhibitor M-11, a 2-Mercaptobenzimidazole Derivative.Int J Mol Sci. 2021 Dec 2;22(23):13061. doi: 10.3390/ijms222313061. Int J Mol Sci. 2021. PMID: 34884863 Free PMC article.
-
Efficient and Explainable Virtual Screening of Molecules through Fingerprint-Generating Networks Integrated with Artificial Neural Networks.ACS Omega. 2025 Jan 28;10(5):4896-4911. doi: 10.1021/acsomega.4c10289. eCollection 2025 Feb 11. ACS Omega. 2025. PMID: 39959102 Free PMC article.
-
Virtual Screening of Molecules via Neural Fingerprint-based Deep Learning Technique.Res Sq [Preprint]. 2024 May 9:rs.3.rs-4355625. doi: 10.21203/rs.3.rs-4355625/v1. Res Sq. 2024. Update in: ACS Omega. 2025 Jan 28;10(5):4896-4911. doi: 10.1021/acsomega.4c10289. PMID: 38766198 Free PMC article. Updated. Preprint.
-
Editing Domain Motions Preorganize the Synthetic Active Site of Prolyl-tRNA Synthetase.ACS Catal. 2020 Sep 4;10(17):10229-10242. doi: 10.1021/acscatal.0c02381. Epub 2020 Aug 14. ACS Catal. 2020. PMID: 34295570 Free PMC article.
References
-
- Sollner S; Macheroux P, New Roles of Flavoproteins in Molecular Cell Biology: An Unexpected Role for Quinone Reductases as Regulators of Proteasomal Degradation. FEBS J. 2009, 276, 4313–4324. - PubMed
-
- Santina E The Potential Role of the Oxidoreductase, NQO2 in Breast Cancer. Doctoral dissertation, University of Manchester, Manchester, September 2015.
-
- Boutin JA, Quinone Reductase 2 as a Promising Target of Melatonin Therapeutic Actions. Expert Opin. Ther. Targets 2016, 20, 303–317. - PubMed
Grants and funding
LinkOut - more resources
Full Text Sources
