Improving the identification of antigenic sites in the H1N1 influenza virus through accounting for the experimental structure in a sparse hierarchical Bayesian model
- PMID: 31598013
- PMCID: PMC6774336
- DOI: 10.1111/rssc.12338
Improving the identification of antigenic sites in the H1N1 influenza virus through accounting for the experimental structure in a sparse hierarchical Bayesian model
Abstract
Understanding how genetic changes allow emerging virus strains to escape the protection afforded by vaccination is vital for the maintenance of effective vaccines. We use structural and phylogenetic differences between pairs of virus strains to identify important antigenic sites on the surface of the influenza A(H1N1) virus through the prediction of haemagglutination inhibition (HI) titre: pairwise measures of the antigenic similarity of virus strains. We propose a sparse hierarchical Bayesian model that can deal with the pairwise structure and inherent experimental variability in the H1N1 data through the introduction of latent variables. The latent variables represent the underlying HI titre measurement of any given pair of virus strains and help to account for the fact that, for any HI titre measurement between the same pair of virus strains, the difference in the viral sequence remains the same. Through accurately representing the structure of the H1N1 data, the model can select virus sites which are antigenic, while its latent structure achieves the computational efficiency that is required to deal with large virus sequence data, as typically available for the influenza virus. In addition to the latent variable model, we also propose a new method, the block-integrated widely applicable information criterion biWAIC, for selecting between competing models. We show how this enables us to select the random effects effectively when used with the model proposed and we apply both methods to an A(H1N1) data set.
Keywords: Antigenic variability; Bayesian hierarchical models; Influenza virus; Latent variable models; Markov chain Monte Carlo sampling; Mixed effects models; Spike‐and‐slab prior; Widely applicable information criterion.
© 2019 The Authors Journal of the Royal Statistical Society: Series C (Applied Statistics) Published by John Wiley & Sons Ltd on behalf of the Royal Statistical Society.
Figures

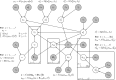
 , the data and fixed (higher order) hyperparameters: ∘, parameters and hyperparameters that are inferred
, the data and fixed (higher order) hyperparameters: ∘, parameters and hyperparameters that are inferred
 ) against the probabilities for a model with a noise structure based on the H1N1 data set (
) against the probabilities for a model with a noise structure based on the H1N1 data set ( ); the results show the probability that the irrelevant variable is included in the model decreases as the number of observations increases for the data with IID Gaussian noise; conversely it shows an increase in the probability of its inclusion as the number of observations increases when there is a noise structure based on the H1N1 data set): (a) 500 observations; (b) 1000 observations; (c) 2000 observations
); the results show the probability that the irrelevant variable is included in the model decreases as the number of observations increases for the data with IID Gaussian noise; conversely it shows an increase in the probability of its inclusion as the number of observations increases when there is a noise structure based on the H1N1 data set): (a) 500 observations; (b) 1000 observations; (c) 2000 observations
 ), biWAIC (
), biWAIC ( ) and Bayesian tenfold ICV (
) and Bayesian tenfold ICV ( ) in terms of correctly selecting random‐effect components for the data set described in Section 6.1.3; the figure takes the results from Table 3
) in terms of correctly selecting random‐effect components for the data set described in Section 6.1.3; the figure takes the results from Table 3

Similar articles
-
Bayesian inference of antigenic and non-antigenic variables from haemagglutination inhibition assays for influenza surveillance.R Soc Open Sci. 2018 Jul 25;5(7):180113. doi: 10.1098/rsos.180113. eCollection 2018 Jul. R Soc Open Sci. 2018. PMID: 30109067 Free PMC article.
-
Computational Identification of Antigenicity-Associated Sites in the Hemagglutinin Protein of A/H1N1 Seasonal Influenza Virus.PLoS One. 2015 May 15;10(5):e0126742. doi: 10.1371/journal.pone.0126742. eCollection 2015. PLoS One. 2015. PMID: 25978416 Free PMC article.
-
Antigenic sites of H1N1 influenza virus hemagglutinin revealed by natural isolates and inhibition assays.Vaccine. 2012 Sep 28;30(44):6327-37. doi: 10.1016/j.vaccine.2012.07.079. Epub 2012 Aug 8. Vaccine. 2012. PMID: 22885274
-
A 1-year follow-on study from a randomised, head-to-head, multicentre, open-label study of two pandemic influenza vaccines in children.Health Technol Assess. 2011 Dec;15(45):v-vi, xi-xiii, 1-128. doi: 10.3310/hta15450. Health Technol Assess. 2011. PMID: 22257497 Clinical Trial.
-
Relationship between haemagglutination-inhibiting antibody titres and clinical protection against influenza: development and application of a bayesian random-effects model.BMC Med Res Methodol. 2010 Mar 8;10:18. doi: 10.1186/1471-2288-10-18. BMC Med Res Methodol. 2010. PMID: 20210985 Free PMC article.
Cited by
-
A Bayesian approach to incorporate structural data into the mapping of genotype to antigenic phenotype of influenza A(H3N2) viruses.PLoS Comput Biol. 2023 Mar 27;19(3):e1010885. doi: 10.1371/journal.pcbi.1010885. eCollection 2023 Mar. PLoS Comput Biol. 2023. PMID: 36972311 Free PMC article.
-
Antigenic characterization of influenza and SARS-CoV-2 viruses.Anal Bioanal Chem. 2022 Apr;414(9):2841-2881. doi: 10.1007/s00216-021-03806-6. Epub 2021 Dec 14. Anal Bioanal Chem. 2022. PMID: 34905077 Free PMC article. Review.
References
-
- Andrieu, C. and Doucet, A. (1999) Joint bayesian model selection and estimation of noisy sinusoids via reversible jump MCMC. IEEE Trans. Signl Process., 47, 2667–2676.
-
- Barr, I. G. , Russell, C. , Besselaar, T. G. , Cox, N. J. , Daniels, R. S. , Donis, R. , Engelhardt, O. G. , Grohmann, G. , Itamura, S. , Kelso, A. , McCauley, J. , Odagiri, T. , Schultz‐Cherry, S. , Shu, Y. , Smith, D. , Tashiro, M. , Wang, D. , Webby, R. , Xu, X. , Ye, Z. and Zhang, W. (2014) WHO recommendations for the viruses used in the 2013‐2014 Northern Hemisphere influenza vaccine: epidemiology, antigenic and genetic characteristics of influenza A(H1N1)pdm09, A(H3N2) and B influenza viruses collected from October 2012 to January 2013. Vaccine, 32, 4713–4725. - PubMed
-
- Caton, A. J. , Brownlee, G. G. , Yewdell, J. W. and Gerhard, W. (1982) The antigenic structure of the influenza virus A/PR/8/34 hemagglutinin (H1 subtype). Cell, 31, part 1, 417–427. - PubMed
-
- Davies, V. (2016) Sparse hierarchical Bayesian models for detecting relevant antigenic sites in virus evolution. PhD Thesis. University of Glasgow, Glasgow.
-
- Davies, V. , Reeve, R. , Harvey, W. T. and Husmeier, D. (2016) Selecting random effect components in a sparse hierarchical Bayesian model for identifying antigenic variability In Computational Intelligence Methods for Bioinformatics and Biostatistics (eds Angelini C., Rancoita P. M. V. and Rovetta S.), pp. 14–27. Cham: Springer.
Grants and funding
LinkOut - more resources
Full Text Sources
