Characteristic scales of Townsend's wall-attached eddies
- PMID: 31631906
- PMCID: PMC6800708
- DOI: 10.1017/jfm.2019.209
Characteristic scales of Townsend's wall-attached eddies
Abstract
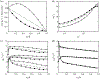
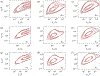
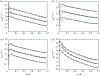
Townsend (The Structure of Turbulent Shear Flow, 1976, Cambridge University Press) proposed a structural model for the logarithmic layer (log layer) of wall turbulence at high Reynolds numbers, where the dominant momentum-carrying motions are organised into a multiscale population of eddies attached to the wall. In the attached-eddy framework, the relevant length and velocity scales of the wall-attached eddies are the friction velocity and the distance to the wall. In the present work, we hypothesise that the momentum-carrying eddies are controlled by the mean momentum flux and mean shear with no explicit reference to the distance to the wall and propose new characteristic velocity, length and time scales consistent with this argument. Our hypothesis is supported by direct numerical simulation of turbulent channel flows driven by non-uniform body forces and modified mean velocity profiles, where the resulting outer-layer flow structures are substantially altered to accommodate the new mean momentum transfer. The proposed scaling is further corroborated by simulations where the no-slip wall is replaced by a Robin boundary condition for the three velocity components, allowing for substantial wall-normal transpiration at all length scales. We show that the outer-layer one-point statistics and spectra of this channel with transpiration agree quantitatively with those of its wall-bounded counterpart. The results reveal that the wall-parallel no-slip condition is not required to recover classic wall-bounded turbulence far from the wall and, more importantly, neither is the impermeability condition at the wall.
Keywords: turbulence simulation; turbulence theory; turbulent boundary layers.
Figures

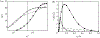

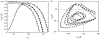

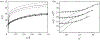


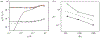

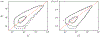



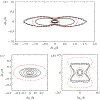
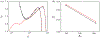
References
-
- Abderrahaman-Elena N & García-Mayoral R 2017. Analysis of anisotropically permeable surfaces for turbulent drag reduction. Phys. Rev. Fluids 2, 114609.
-
- Adrian RJ 2007. Hairpin vortex organization in wall turbulence. Phys. Fluids 19 (4), 041301.
-
- Adrian RJ, Meinhart CD & Tomkins CD 2000. Vortex organization in the outer region of the turbulent boundary layer. J. Fluid Mech. 422, 1–54.
-
- Afzal N 1976. Millikan’s argument at moderately large Reynolds number. Phys. Fluids 19 (4), 600–602.
-
- Afzal N & Yajnik K 1973. Analysis of turbulent pipe and channel flows at moderately large Reynolds number. J. Fluid Mech. 61 (1), 23–31.
Grants and funding
LinkOut - more resources
Full Text Sources
