Optical vortices 30 years on: OAM manipulation from topological charge to multiple singularities

Abstract

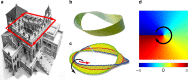
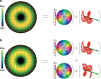
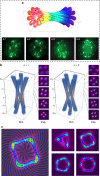
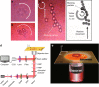
Thirty years ago, Coullet et al. proposed that a special optical field exists in laser cavities bearing some analogy with the superfluid vortex. Since then, optical vortices have been widely studied, inspired by the hydrodynamics sharing similar mathematics. Akin to a fluid vortex with a central flow singularity, an optical vortex beam has a phase singularity with a certain topological charge, giving rise to a hollow intensity distribution. Such a beam with helical phase fronts and orbital angular momentum reveals a subtle connection between macroscopic physical optics and microscopic quantum optics. These amazing properties provide a new understanding of a wide range of optical and physical phenomena, including twisting photons, spin-orbital interactions, Bose-Einstein condensates, etc., while the associated technologies for manipulating optical vortices have become increasingly tunable and flexible. Hitherto, owing to these salient properties and optical manipulation technologies, tunable vortex beams have engendered tremendous advanced applications such as optical tweezers, high-order quantum entanglement, and nonlinear optics. This article reviews the recent progress in tunable vortex technologies along with their advanced applications.

Keywords: Optical physics.

Fig. 1. Roadmap of the 30-year development of optical vortices from 1989 to 2019, including significant theoretical and technical breakthroughs with corresponding references.

Reprinted with permission from ref. , Copyright (2019), with permission from Elsevier. Reprinted with permission from refs. ^,,,,,,,. Copyright (2019) by the American Physical Society. From refs. ^,,,,,,,. Reprinted with permission from AAAS. Reprinted by permission from Springer Nature: Nature^,,,, Nature Physics^,, Nature Photonics^,,, Nature Communications^,, Light: Science & Applications, Copyright (2019). From ref. . Reproduced by permission of IOP Publishing

Fig. 2. Basic topological structure of vortex from art to science.

The topological structures of a the Penrose Stair, b, c a Möbius strip, and d the phase of a vortex soliton (Hilbert factor) are isomorphic, i.e., a physical value (displacement or angle) continually increases along a closed loop and coincides exactly with the origin after a roundtrip. c From ref. . Reprinted with permission from AAAS

Fig. 3. The OAM of light beams is revealed by the phase distributions and the SAM by the polarizations.

The phase distributions for various eigenstates of OAM and the polarizations (right- and left-handed circularly polarized) for the two eigenstates of SAM are illustrated

Fig. 4. Formation of vector beam with space-polarization nonseparability.

a Circularly polarized OV with an azimuthally varying phase distribution. Such a state is considered separable, as it can be represented as the product of a spatially varying vortex phase and a polarization state vector. b Spider-like vector vortex represented as the superposition of the state of a with another state with the opposite phase variation and the opposite circular polarization. From ref. . Reprinted with permission from AAAS

Fig. 5. Decomposition of LG vortex beams.

Examples of the decomposition of LG modes (LG_0,1 (a) and LG_0,2 (b)) into HG modes according to Eq. (7), where the insets in the dotted box show the corresponding vortex phase distributions

Fig. 6. Classical models of paraxial VBs.

a Evolution of the (I) intensity and (II) phase distributions of HLG modes as interposed states between HG and LG modes; b various (I) intensity and (II) phase distributions of IG and HLG modes; c intensity distributions of a selection of (I) odd and (II) helical Mathieu beams. (I) Intensity and (II) phase distributions of SU(2) vortex geometric modes for Ω = 1/4 (d) and Ω = 1/3 (e). SHEN spheres with orders of (n, m) = (3, 1) (f) and (n, m) = (0, 6) (g) along with represented mode (phase) fields at selected points. b Reproduced from ref. , with the permission of AIP Publishing. c Reprinted with permission from ref. , OSA Publishing. d, e Reprinted with permission from ref. , OSA Publishing. f, g Reprinted with permission from ref. , OSA Publishing

Fig. 7. Classical models of spatial nonparaxial OVs.

Polarization topology of optical Möbius strips with twisted TCs of –1/2 and –3/2 (a, b). Nodal trefoil knot and pigtail braid knot OVs (c, d) and corresponding phase distributions (e, f). Optical vortex knots of a threefold distorted loop (g), a trefoil knot (h), and a pair of linked rings (i). a, b From ref. . Reprinted with permission from AAAS. c–f Reprinted by permission from Nature Physics, Copyright (2019). g–i Reprinted by permission from Nature Physics, Copyright (2019)

Fig. 8. Reflection, interference, diffraction, and polarization of VBs.

a Abnormal reflection of a VB. b LG VBs with different TCs (first column) and corresponding interference patterns with a co-axis coherent planar wave (second column) and an inclined coherent planar wave (third column). Far-field diffraction patterns of VBs through a triangular aperture (c) and a single slit (d). e Near-field diffraction pattern of a VB. f Polarization distribution of vector VBs on the HPS. a Reprinted with permission from ref. . Copyright (2019) by the American Physical Society. c Reprinted with permission from ref. . Copyright (2019) by the American Physical Society. d Reprinted with permission from ref. , Copyright (2019), with permission from Elsevier. f Reprinted by permission from Nature Photonics, Copyright (2019)

Fig. 9. Generation of wavelength- and OAM-tunable CW VBs (I).

Generation methods of wavelength- and OAM-tunable VBs using an acousto-optic fibre grating (a), along with the experimental results (b), an SPP-embedded MEMS filter system (c–e), and a VBG in a hollow-pumped solid-state laser (f). Reprinted with permission from refs. ^–, OSA Publishing

Fig. 10. Generation of wavelength- and OAM-tunable CW VBs (II).

Generation methods of wavelength- and OAM-tunable VBs using a dual-off-axis pumped Yb:CALGO laser system^, (a), intracavity birefringent plate rotation (b), and a “Gauss-OAM-Gauss” beam conversion system in a fibre laser (c). a From refs. ^,. Reproduced by permission of IOP Publishing. b Reprinted with permission from ref. , OSA Publishing

Fig. 11. Generation of wavelength- and OAM-tunable pulsed VBs.

Generation methods of a room-temperature diode-pumped Er,Yb:glass microchip nanosecond laser (a), picosecond-level VBs in a self-mode-locked Nd:YVO₄ laser (b), and femtosecond VBs in an SESAM mode-locking laser (c). a ©(2019) IEEE. Reprinted, with permission, from ref. . b Reprinted with permission from ref. , OSA Publishing. c From ref. . Reproduced by permission of IOP Publishing

Fig. 12. Exotic SU(2) structured multi-singularity VBs.

Theoretical and experimental investigations of special multi-singularity VBs: a trochoidal vortex modes, b the vortex SU(2) GM, and c polygonal VBs. a Reprinted with permission from ref. . Copyright (2019) by the American Physical Society. b Reprinted with permission from ref. , OSA Publishing. c © (2019) IEEE. Reprinted, with permission, from ref.

Fig. 13. Generation of multi-singularity VBs.

a Exploring the singularity splitting phenomenon in AMC systems. b Multiple singularity formation in fractional OAM VBs. Tailoring multi-singularity beams with c a circular vortex array and d an optical vortex array along an arbitrary curvilinear arrangement. a Reprinted with permission from ref. , Copyright (2019), with permission from Elsevier. b Reprinted with permission from ref. , OSA Publishing. c Reprinted with permission from ref. . Copyright (2019) by John Wiley and Sons. d Reprinted with permission from ref. , OSA Publishing

Fig. 14. Optical tweezers with VBs can manipulate not only the positions of particles but also their motion, such as precession, nutation, spin, and more complicated orbital motion²¹⁷.

Reprinted by permission from Springer Nature: Nature Photonics, Copyright (2019)

Fig. 15. Particle manipulation using OVs.

a, b Manipulating the rotation of multiple particles and c aligning and transporting particles with fractional VBs. d Setup and e schematic of plasmonic vortex tweezers for manipulating metal particles. a–c Reprinted with permission from ref. , OSA Publishing

Fig. 16. Optical communication using OVs.

a Optical communication can be realized by modulating the time domain, frequency domain, amplitude, polarization, and OAM. b Schematic of sidelobe-modulated OVs for free-space communication. c Dammann-grating-enabled OAM multiplexing technology raising the large capacity to the Pbit level. d Underwater optical communication using VBs. b Reprinted with permission from ref. , OSA Publishing. c Reprinted by permission from Springer Nature: Light: Science & Applications, Copyright (2019)

Fig. 17. Quantum technologies using OVs.

a OAM-entanglement photon pairs generated by the spontaneous parametric down conversion process. b Quantum tomography experimental data demonstrating that the OAM of the pump beam is transferred to the sum of the OAM of the generated photons (m_p = m₁ + m₂). c Setup for quantum digital spiral imaging. Comparison between quantum communication using d entangled photons and e non-separable states of vector OVs. b Reprinted by permission from Springer Nature: Nature Physics, Copyright (2019). c Reprinted by permission from Springer Nature: Light: Science & Applications, Copyright (2019). d, e Reprinted by permission from Springer Nature: Nature Physics, Copyright (2019)

Fig. 18. High-resolution imaging using OVs.

a Setup of the plasmonic structured illumination microscopy technique, and b imaging results with super-resolution. c Setup of superoscillation focusing imaging using a vector VB, and d imaging results with super-resolution. a, b Reprinted with permission from ref. , OSA Publishing. c, d Reprinted with permission from ref. , OSA Publishing

Fig. 19. Nanotechnology, nonlinear conversion, and detection using OVs.

a Various integrated nanoscale vortex emitters. b Sorting and resolving enantiomers or molecules with different chiralities. c Machining a nanoscale needle using VBs with d clockwise rotation and e counterclockwise rotation structures. f Schematic diagram of the rotational Doppler effect in nonlinear optics. g Schematic diagram of the OAM conservation process in the high-harmonic generation of VBs. h Schematic diagram of object detection using the OAM spectrum. a From ref. . Reprinted with permission from AAAS. b Reprinted/adapted from ref. . © The Authors, some rights reserved; exclusive licensee American Association for the Advancement of Science. Distributed under a Creative Commons Attribution NonCommercial License 4.0 (CC BY-NC) http://creativecommons.org/licenses/by-nc/4.0/. c–e Reprinted with permission from ref. , OSA Publishing. f Reprinted by permission from Springer Nature: Nature Physics, Copyright (2019). g Reprinted by permission from Springer Nature: Nature Communications, Copyright (2019). h Reprinted with permission from ref. , OSA Publishing

Fig. 20. Metrology and astronomy using OVs.

a VBs can be used to detect the spin motion of an object. b Twisted light can be used for label-free single-molecule detection. c VBs can be used with plasmonic nanoslit structures for multi-channel OAM generation and detection. d Vortex generation around a rotating black hole. e–g Imaging of an OV coronagraph. a From ref. . Reprinted with permission from AAAS. b Reprinted by permission from Springer Nature: Nature Materials, Copyright (2019). c Reprinted with permission from ref. . Copyright (2019) by John Wiley and Sons. d Reprinted by permission from Springer Nature: Nature Physics, Copyright (2019). e–g Reprinted with permission from ref. , OSA Publishing