The Wiring of Intelligence
- PMID: 31647746
- PMCID: PMC7433699
- DOI: 10.1177/1745691619866447
The Wiring of Intelligence
Abstract
The positive manifold of intelligence has fascinated generations of scholars in human ability. In the past century, various formal explanations have been proposed, including the dominant g factor, the revived sampling theory, and the recent multiplier effect model and mutualism model. In this article, we propose a novel idiographic explanation. We formally conceptualize intelligence as evolving networks in which new facts and procedures are wired together during development. The static model, an extension of the Fortuin-Kasteleyn model, provides a parsimonious explanation of the positive manifold and intelligence's hierarchical factor structure. We show how it can explain the Matthew effect across developmental stages. Finally, we introduce a method for studying growth dynamics. Our truly idiographic approach offers a new view on a century-old construct and ultimately allows the fields of human ability and human learning to coalesce.
Keywords: child development; cognition; idiographic science; individual differences; intelligence; network model; quantitative methodology.
Conflict of interest statement
Figures

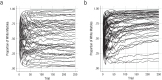


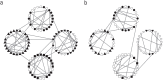




Update of
References
-
- Ackerman P. L., Lohman D. F. (2003). Education and g. In Nyborg H. (Ed.), The scientific study of general intelligence (pp. 275–292). Amsterdam, the Netherlands: Elsevier BV.
-
- Bartholomew D. J. (2004). Measuring intelligence. New York, NY: Cambridge University Press.
-
- Bartholomew D. J., Allerhand M., Deary I. J. (2013). Measuring mental capacity: Thomsons bonds model and Spearmans g-model compared. Intelligence, 41, 222–233. doi:10.1016/j.intell.2013.03.007 - DOI
-
- Bartlett F. C. (1932). Remembering: A study in experimental and social psychology. Retrieved from https://archive.org/details/rememberingstudy00bart
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Medical
Miscellaneous

