Integrating the underlying structure of stochasticity into community ecology

Abstract

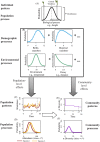
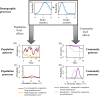
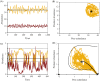
Stochasticity is a core component of ecology, as it underlies key processes that structure and create variability in nature. Despite its fundamental importance in ecological systems, the concept is often treated as synonymous with unpredictability in community ecology, and studies tend to focus on single forms of stochasticity rather than taking a more holistic view. This has led to multiple narratives for how stochasticity mediates community dynamics. Here, we present a framework that describes how different forms of stochasticity (notably demographic and environmental stochasticity) combine to provide underlying and predictable structure in diverse communities. This framework builds on the deep ecological understanding of stochastic processes acting at individual and population levels and in modules of a few interacting species. We support our framework with a mathematical model that we use to synthesize key literature, demonstrating that stochasticity is more than simple uncertainty. Rather, stochasticity has profound and predictable effects on community dynamics that are critical for understanding how diversity is maintained. We propose next steps that ecologists might use to explore the role of stochasticity for structuring communities in theoretical and empirical systems, and thereby enhance our understanding of community dynamics.

Keywords: autocorrelation; demographic stochasticity; distribution; diversity; environmental stochasticity; population dynamics; scale; uncertainty.

Figure 1

The three forms of stochasticity and how they influence observed population and community data. Data observations (A) are influenced by stochasticity in three general forms: demographic (e.g., stochasticity in intrinsic processes such as birth and deaths), environmental (e.g., stochasticity in extrinsic environmental conditions such as rainfall and temperature), and measurement error (e.g., imprecise data collection). Both demographic (B) and environmental (C) stochasticity represent biologically meaningful forms of uncertainty. Organisms in the environment experience these forms of stochasticity simultaneously (D), resulting in a multidimensional distribution of vital rates. Measurement error increases variability in observed data by creating error (E, F) around the underlying multidimensional distribution (D).

Figure 2

Visualization of our conceptual framework. Here we demonstrate the basic principles of our framework for examining the role of stochasticity in communities, as described in detail in Box 1. Direct applications of the framework occur in Figs. 3, 4, 5.

Figure 3

Incorporating both demographic and environmental stochasticity concurrently. Even when incorporating relatively simple demographic (A) and environmental (B) stochastic processes, observed community patterns (C) and their underlying distributions (D) differ when considering only a single type of stochasticity rather than their combination. Model parameters are $a=0$ (no autocorrelation), $\mathrm{\zeta }=0.35$, $R_i\sim \text{Uniform}(2,2.5)$ ${\mathrm{\alpha }}_{\mathit{ij}}\sim \text{Uniform}(0.005,0.01$) when $i\ne j$, and ${\mathrm{\alpha }}_{\mathit{ii}}=0.03$ for all i, j (Eqs. (5), (6), (7), (8)). Distributions of expected diversity are created at time point t = 40 by examining observed diversity across 1,000 runs.

Figure 4

Modeling demographic stochasticity in populations and communities. Modeled effects of demographic stochasticity (A) alter both population abundance and community diversity patterns. In accordance with the literature, we focus on the interaction of demographic stochasticity with carrying capacity in populations and intra‐ and interspecific competition in communities. At the population level, persistence time declines with increasing demographic stochasticity in small populations (B), as the distribution of expected species abundances decreases with decreasing population size (C). At the community level, observed alpha diversity (D) is expected to be more variable and decline faster over time when intraspecific competition ≈ interspecific competition than when the strength of interspecific competition is less than that of intraspecific competition (E). Population model parameters are $R_1=R_2=1.6$, ${\mathrm{\alpha }}_1=0.02$, ${\mathrm{\alpha }}_2=0.1$ (Eq. 2). Community model parameters are (1) purple line $R_i\sim \text{Uniform}(2.0,2.5)$ ${\mathrm{\alpha }}_{\mathit{ij}}\sim \text{Uniform}\left(0.002,0.005\right)$ when $i\ne j$, and ${\mathrm{\alpha }}_{\mathit{ii}}=0.03$ and (2) pink line $R_i=\overline{R}$ from the purple line and ${\mathrm{\alpha }}_{\mathit{ij}}=\overline{{\mathrm{\alpha }}_{\mathit{ij}}}$ from the purple line for all i, j (Eq. 6) where the overbar denotes the mean.

Figure 5

Modeling environmental stochasticity in populations and communities. Modeled effects of autocorrelation in environmental stochasticity (A) alters population and community patterns ($a=0$ for white noise; $a=0.75$ for red noise). In compensatory populations, increasing the strength of positive autocorrelation in environmental stochasticity increases the correlation in population size between time steps (B, C). In contrast, in communities where environmental stochasticity alters the germination rate from the seedbank, environmental autocorrelation has a more minimal effect, but increasing the strength of positive autocorrelation in environmental stochasticity slightly decreases expected diversity (D, E). Population model parameters are $R=1.5,\mathrm{\zeta }=0.25,$ and $\mathrm{\alpha }=0.05$ (Eq. 3). Community model parameters are $s_i=0.8,g_i=0.5,\mathrm{\zeta }=0.2,R_i\sim \text{Uniform}(1.1,1.5)$ and ${\alpha }_{\mathit{ij}}\sim \text{Uniform}(0.001,0.005)$ when $i\ne j$, and ${\mathrm{\alpha }}_{\mathit{ii}}=0.007$ (Eq. 7).

Figure 6

The role of stochasticity in transient dynamics. Predator–prey dynamics, plotted both as time series (left) and as phase diagrams (right), with stochastic trajectories shown in yellow or red and deterministic trajectories in black or gray. (A) The deterministic model (deterministic prey dynamics in black and deterministic predator dynamics in gray) shows transient cycles. In the presence of environmental stochasticity (stochastic prey dynamics in yellow and stochastic predator dynamics in red), the cycles are sustained. Here, stochasticity prevents the populations from settling onto their deterministic equilibrium and the cycles that were transient in the deterministic case are perpetuated forever. (B) The same dynamics in state space, with a stochastic trajectory in yellow and a deterministic one in black. (C) Another stochastic predator–prey model, illustrating how stochasticity can reveal unstable features in the underlying deterministic structure. Without stochasticity (black and gray lines), the populations show transient cycles then settle onto a stable coexistence equilibrium. An unstable equilibrium exists at the dashed black line (for the prey) and the x‐axis (for the predator). With stochasticity (red and yellow trajectories), the populations visit both the stable and unstable equilibria. Thus, the stochastic dynamics can reveal the unstable states in a system. (D) shows these dynamics in state space, with the deterministic equilibria marked: the dot is the stable equilibrium and Xs are unstable (saddle) points. Models are described in Appendices S3 and S5.