Critical dependence of morphodynamic models of fluvial and tidal systems on empirical downslope sediment transport

Abstract

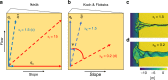
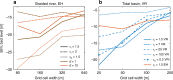
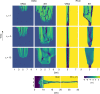
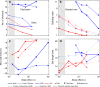
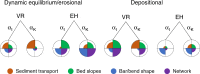
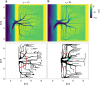
The morphological development of fluvial and tidal systems is forecast more and more frequently by models in scientific and engineering studies for decision making regarding climate change mitigation, flood control, navigation and engineering works. However, many existing morphodynamic models predict unrealistically high channel incision, which is often dampened by increased gravity-driven sediment transport on side-slopes by up to two orders of magnitude too high. Here we show that such arbitrary calibrations dramatically bias sediment dynamics, channel patterns, and rate of morphological change. For five different models bracketing a range of scales and environments, we found that it is impossible to calibrate a model on both sediment transport magnitude and morphology. Consequently, present calibration practice may cause an order magnitude error in either morphology or morphological change. We show how model design can be optimized for different applications. We discuss the major implications for model interpretation and a critical knowledge gap.

Fig. 1

Literature inventory of slope effects in morphodynamic models. a Model studies that mentioned, discussed, or overlooked the severe channel incision and the artificial increase in slope effect that was necessary to counteract this (see Supplementary Information for inventory). b Studies that mention the magnitude of the slope effect subdivided by modeled environment and the applied slope effect value (1 = default)

Fig. 2

Schematic drawing of the two main slope parameterizations. The parameterizations for sediment deflection by Ikeda (${\alpha }_{\mathrm{I}}$) and Koch and Flokstra (${\alpha }_{\mathrm{K}}$) drawn on a transverse bed slope. Both methods are drawn on a top view of a bed sloping toward the right. Blue solid arrows show sediment transport in streamwise direction ($q_{\mathrm{s}}$) and transverse direction ($q_n$, only for Ikeda), and dashed blue arrows show the resulting transport vectors ($q$) with default values for the slope effect. Red arrows represent transport vectors when the slope effect is increased to typical values used in current model studies. a The method of Ikeda increases the transverse sediment vector as a function of slope and ${\alpha }_{\mathrm{I}}$ and thereby increases the resulting sediment transport vector. b The method of Koch and Flokstra rotates the streamwise transport vector over an angle ($\psi$) as a function of slope and ${\alpha }_{\mathrm{K}}$. ${\alpha }_{\mathrm{K}}$ is roughly the inverse of ${\alpha }_{\mathrm{I}}$. See Supplementary Note 1 for detailed calculation method and how to translate ${\alpha }_{\mathrm{K}}$ into ${\alpha }_{\mathrm{I}}$. c, d Examples of a modeled river delta for default (${\alpha }_{\mathrm{I}}$ = 1.5) and high (${\alpha }_{\mathrm{K}}$ = 0.2) slope effect (see Supplementary Fig. 6 for more examples)

Fig. 3

Overview of model environments and objectives in this study. The narrow channel model and the river in the delta model are used to study local sediment transport processes. The delta model, the braided river model, and the tidal basin model quantify the effects of different slope parameterizations and magnitudes in combination with different sediment transport predictors on bifurcation dynamics, braiding index, and channel dimensions. The calibrated Western Scheldt estuary model shows differences in dynamics between models with different slope parameterizations and magnitudes relevant for fairway dredging depth and intensity

Fig. 4

Influence of slope effect and transport predictor on morphology. Morphology of eight braided river model runs for different combinations of slope effect and sediment transport predictors. Models on the horizontal axis have equal slope effect. The ${\alpha }_{\mathrm{I}}$ is the input parameter of the method of Ikeda, while the ${\alpha }_{\mathrm{K}}$ is the input parameter of the method of Koch and Flokstra, both with defaults of order 1. The graph shows the cumulative distribution of the slopes of all grid cells in the same models at the same timestep. Solid lines are results with IK and dashed lines are results with KF. Colors indicate equal transverse sediment transport magnitudes and the same sediment transport predictor

Fig. 5

Grid size-dependent incision. Tendency to incise quantified as 95% depth against size of the grid cells for different magnitudes of slope effect, of a the braided river model in combination with the sediment transport predictor of Engelund–Hansen, and a horizontal eddy diffusivity $d$ of 1 or 10, and b the tidal basin model

Fig. 6

Effect of grid size-dependent incision on channel dynamics. Development of the bathymetry of a cross-section at the river and at the delta over time in the delta model, for different combinations of sediment transport predictor and magnitude of the slope parameter with the method of Ikeda

Fig. 7

Relation between slope effect and morphodynamic element dimensions. a Number of channels at the delta front in the delta models, and the number of channels in the tidal basin models, against increasing slope effect. b Braiding index with increasing slope effect in the braided river model, with the semi-analytical predictor for braiding index from Crosato and Mosselman in corresponding colors for comparison. c The 95% depth of all tidal channels in the tidal basin models against slope effect. d Mean bar length in the braiding river model when increasing the slope effect, including the predictor of Struiksma and others for wave lengths of bars. Braiding index and bar length are computed according to the methods described in Schuurman et al.. The method of determining the number of channels in the tidal basin models is explained in the “Methods” section. Slope effect is given as the ${\alpha }_{\mathrm{I}}$ for IK and transformed for KF

Fig. 8

Model design recommendations. Relative performance for each combination of transport predictor and slope method in models of either erosive or balanced environments where bank erosion is necessary or depositional environments. Relative performance is divided into four categories, such that the choice of predictors can be made depending on the research objective. Network characteristics include braiding index and the number of channels in, e.g., a tidal basin or a delta

Fig. 9

Bathymetries of the tidal inlet model. Bathymetries are shown for models with the IK parameterization in combination with an ${\alpha }_{\mathrm{I}}$ of a 1.5 (default) and b 25 and their corresponding binary image, where channels are black and the surrounding area is white