Generation of concentric perfect Poincaré beams

Abstract

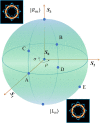
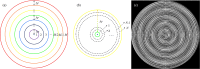
We theoretically propose and experimentally verify a method to generate new polycyclic beams, namely concentric perfect Poincaré beams (CPPBs), by using an encoded annular phase mask. The proposed beams consisting of multiple polarization structured fields can be simultaneously generated in one concentric mode, which are respectively mapped by fundamental Poincaré sphere (PS), high-order Poincaré sphere (HOPS), and hybrid-order Poincaré sphere (HyPS). Moreover, the ring radius, numbers and polarization orders of the CPPBs at arbitrary positions on arbitrary PS are independently controlled. This work enriches the mode distributions of perfect vortex and introduces a new polarization degree of freedom, which has the potential to implement more information beyond the orbital angular momentum multiplexing in optical communication.

Figure 1

Schematic illustration of the arbitrary order PS. The north pole and south pole represent the right and left circularly polarized vortex beams with topological charges of m and n, respectively. Point A(0, 0), B(π, 0), C(0, π/6), D(π, −π/6) and E(π/2, −π/4) represent different states of polarization on the surface of arbitrary order PS.

Figure 2

(a) The states of polarization of Point A (0, 0), B (π, 0), C (0, π/6), D (π, −π/6) and E(π/2, −π/4) on the surface of fundamental PS (m = n = 1), HOPS (−m = n = 1), and HyPS (m = −1, n = 3). (b) Stokes parameters S₀, S₁, S₂, and S₃ of different Poincaré spheres at point A.

Figure 3

Schematic diagram of the encoded annular phase mask.

Figure 4

Experiment setup of the proposed CPPBs system.

Figure 5

From left to right, the generated PPBs with different ring radius are shown in the upper row. In the bottom row, different numbers of ring are shown.

Figure 6

The CPPBs at different points on the surface of arbitrary order PS are generated when m₁ = n₁ = 1, −m₂ = n₂ = 1, m₃ = −1, n₃ = 3. Point A, B, C, D and E are illustrated in (a–e), respectively. From left to right are the recorded patterns by CCD with a rotating polarizer P2. The corresponding experimental normalized Stokes parameters of CPPBs are shown in the last column.

Figure 7

Three CPPBs with different topological charges. In (a), simulation and experimental results of the three CPPBs are shown when m₁ = n₁ = 1, m₃ = −3, n₃ = 4. In (b), simulation and experimental results of the three CPPBs are shown when m₁ = n₁ = 1, −m₂ = n₂ = 3. From left to right are the recorded patterns by CCD without or with a rotating polarizer. The Stokes parameters are shown in the last three columns.