Synchronization transitions caused by time-varying coupling functions
- PMID: 31656137
- PMCID: PMC6834000
- DOI: 10.1098/rsta.2019.0275
Synchronization transitions caused by time-varying coupling functions
Abstract
Interacting dynamical systems are widespread in nature. The influence that one such system exerts on another is described by a coupling function; and the coupling functions extracted from the time-series of interacting dynamical systems are often found to be time-varying. Although much effort has been devoted to the analysis of coupling functions, the influence of time-variability on the associated dynamics remains largely unexplored. Motivated especially by coupling functions in biology, including the cardiorespiratory and neural delta-alpha coupling functions, this paper offers a contribution to the understanding of effects due to time-varying interactions. Through both numerics and mathematically rigorous theoretical consideration, we show that for time-variable coupling functions with time-independent net coupling strength, transitions into and out of phase- synchronization can occur, even though the frozen coupling functions determine phase-synchronization solely by virtue of their net coupling strength. Thus the information about interactions provided by the shape of coupling functions plays a greater role in determining behaviour when these coupling functions are time-variable. This article is part of the theme issue 'Coupling functions: dynamical interaction mechanisms in the physical, biological and social sciences'.
Keywords: coupled oscillators; coupling functions; dynamical systems; interactions.
Conflict of interest statement
The authors declare that they have no competing interests.
Figures
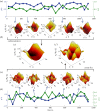
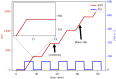
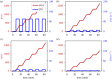
References
-
- Zhang G, Ma J, Alsaedi A, Ahmad B, Alzahrani F. 2018. Dynamical behavior and application in Josephson junction coupled by memristor. Appl. Math. Comput. 321, 290–299. (10.1016/j.amc.2017.10.054) - DOI
-
- Cessac B. 2010. A view of neural networks as dynamical systems. Intern. J. Bifurc. Chaos 20, 1585–1629. (10.1142/S0218127410026721) - DOI
-
- Ma J, Mi L, Zhou P, Xu Y, Hayat T. 2017. Phase synchronization between two neurons induced by coupling of electromagnetic field. Appl. Math. Comput. 307, 321–328. (10.1016/j.amc.2017.03.002) - DOI
MeSH terms
LinkOut - more resources
Full Text Sources
