The Rise of (Chiral) 3D Mechanical Metamaterials

Abstract

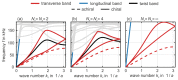
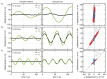
On the occasion of this special issue, we start by briefly outlining some of the history and future perspectives of the field of 3D metamaterials in general and 3D mechanical metamaterials in particular. Next, in the spirit of a specific example, we present our original numerical as well as experimental results on the phenomenon of acoustical activity, the mechanical counterpart of optical activity. We consider a three-dimensional chiral cubic mechanical metamaterial architecture that is different from the one that we have investigated in recent early experiments. We find even larger linear-polarization rotation angles per metamaterial crystal lattice constant than previously and a slower decrease of the effects towards the bulk limit.

Keywords: acoustical activity; chirality; mechanical metamaterials.

Figure 1

(a) and (b) are different views onto the blueprint of one cubic unit cell of the 3D chiral mechanical metamaterial lattice considered here. The indicated geometrical parameters are: $a=250 \mathsf{\mu }\mathrm{m}$, $b=10 \mathsf{\mu }\mathrm{m}$, $c=50 \mathsf{\mu }\mathrm{m}$, and $d=6.25 \mathsf{\mu }\mathrm{m}$. Parameters of the constituent polymer material are: Young’s modulus (or storage modulus) $E=4.18 \mathrm{GPa}$, Poisson’s ratio $\nu =0.4$, and mass density $\rho =1.15\mathrm{g}/{\mathrm{cm}}^3$ (cf. [21]). For some of the calculations, we have added an imaginary part (or loss modulus) of $0.20 \mathrm{GPa}$ to the quoted real part of the polymer Young’s modulus. Whenever applicable, we will explicitly mention this finite imaginary part, which describes damping of the elastic waves.

Figure 2

Calculated phonon band structures of metamaterial beams with a cross section of $N_x\times N_y$ unit cells in the $xy$-plane and with $N_z=\infty$ for wave vectors, $\overrightarrow{k}$, along the $z$ -direction, i.e., $\overrightarrow{k}=\left(0,0,k_z\right)$ with wave number $k_z$. (a) $N_x=N_y=2$, (b) $N_x=N_y=4$, and (c) bulk with $N_x=N_y=\infty$. The transverse (or shear or flexural) bands are highlighted in red. Without chirality, the two transverse bands would be degenerate due to the four-fold rotational symmetry of the metamaterial crystal (see dashed red curves). The blue bands correspond to longitudinal-like (or pressure-like) and the black bands to twist-like modes, respectively. The higher bands are not important in the context of this paper and are plotted in light gray for clarity. Parameters have been given in Figure 1; the imaginary part of the polymer Young’s modulus is set to zero. In panel (a), the maximum splitting of the red bands, $\Delta k_z$, is about half of $\pi /a$, corresponding to a rotation angle of about $45°$ per lattice constant, which approach the fundamental bound of $90°$ per lattice constant.

Figure 3

Calculated bulk phonon band structures (i.e., $N_x=N_y=N_z \to \infty )$ for the metamaterial defined in Figure 1. The lattice constant $a$ and the other parameters are the same as in Figure 2c, where $c/a=0.2$, but we vary the $c/a$ ratio (as indicated). The bands are colored as in Figure 2. In particular, the chiral transverse acoustical bands are again highlighted in red. (a) $c/a=0.1$, (b) $c/a=0.2$, (c) $c/a=0.3$, (d) $c/a=0.4$, (e) $c/a=0.5$, (f) $c/a=0.6$, (g) $c/a=0.7$, and (h) $c/a=0.8$. For each $c/a$ ratio, an inset illustrates the corresponding metamaterial unit cell.

Figure 4

Selected oblique-view electron micrographs of a 3D chiral cubic polymer metamaterial sample manufactured by standard 3D laser micro-printing, following the blueprint illustrated in Figure 1. (a) Total view onto one metamaterial sample with $N_x\times N_y\times N_z=5\times 5\times 12$ unit cells and the bottom sample holder. Here, we use no plate at the top. (b) Zoom-in, showing the intricate interior composed of sets of twisted rods.

Figure 5

Measured displacement-vector components (black and green) versus time, taken at the sample bottom (left column) and at the top of the sample (middle column), respectively for three different frequencies f. The right column shows the $y$-component versus the $x$ -component for the bottom (blue) as well as for the top (red). The sample is excited at its bottom by a piezoelectric transducer with (a) $f=10 \mathrm{kHz}$, (b) $f=20 \mathrm{kHz}$, and (c)$f=30 \mathrm{kHz}$. The metamaterial beam has a cross section of $N_x\times N_y=3\times 3$ unit cells and a height of $N_z=12$ unit cells. From these example data, we derive a polarization rotation angle of (a) $\phi =2°$, (b) $\phi =32°$, and (c) $\phi =43°$.

Figure 6

Derived from data like those shown in Figure 5, we plot the rotation angle $\phi =\phi \left(f\right)$ versus excitation frequency f for different beam cross sections, $\left(N_x\times N_y\right)a^2$, and for different numbers of unit cells, $N_z$, along the propagation direction. The measured results are depicted as circles; the solid curve has been obtained from numerical finite-element frequency-domain calculations for finite-size samples (as in the experiment, cf. Figure 5), accounting for a finite imaginary part of the Young’s modulus $E$ (cf. Figure 1); and the dashed curves have been obtained from phonon band-structure calculations (cf. Figure 2), assuming zero imaginary part of $E$. In the upper right-hand side panel, we vary $N_z$ at fixed $N_x=N_y$. In the lower right-hand side panel, we show by the dashed black curve the expectation for the bulk limit, obtained from phonon band-structure calculations, again with zero imaginary part of $E$. Obviously, the $N_x\times N_y=5\times 5$ case (blue) is already very close to the bulk limit (dashed back curve). At around $f=100 \mathrm{kHz}$, we obtain a polarization rotation as large as about $30°$ per lattice constant.