Estimating the Readily-Releasable Vesicle Pool Size at Synaptic Connections in the Neocortex
- PMID: 31680928
- PMCID: PMC6813366
- DOI: 10.3389/fnsyn.2019.00029
Estimating the Readily-Releasable Vesicle Pool Size at Synaptic Connections in the Neocortex
Abstract
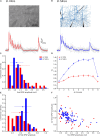
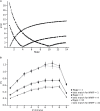
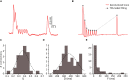
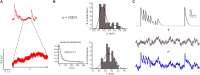
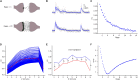
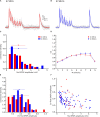
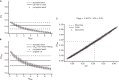
Previous studies based on the 'Quantal Model' for synaptic transmission suggest that neurotransmitter release is mediated by a single release site at individual synaptic contacts in the neocortex. However, recent studies seem to contradict this hypothesis and indicate that multi-vesicular release (MVR) could better explain the synaptic response variability observed in vitro. In this study we present a novel method to estimate the number of release sites per synapse, also known as the size of the readily releasable pool (NRRP), from paired whole-cell recordings of connections between layer 5 thick tufted pyramidal cell (L5_TTPC) in the juvenile rat somatosensory cortex. Our approach extends the work of Loebel et al. (2009) by leveraging a recently published data-driven biophysical model of neocortical tissue. Using this approach, we estimated NRRP to be between two to three for synaptic connections between L5_TTPCs. To constrain NRRP values for other connections in the microcircuit, we developed and validated a generalization approach using published data on the coefficient of variation (CV) of the amplitudes of post-synaptic potentials (PSPs) from literature and comparing them against in silico experiments. Our study predicts that transmitter release at synaptic connections in the neocortex could be mediated by MVR and provides a data-driven approach to constrain the MVR model parameters in the microcircuit.
Keywords: mathematical model; multi vesicular release; neocortex; quantal analysis; short-term depression; synaptic transmission.
Copyright © 2019 Barros-Zulaica, Rahmon, Chindemi, Perin, Markram, Muller and Ramaswamy.
Figures
References
-
- Bibbona E. (2008). The Ornstein-Uhlenbeck process as a model of a low-pass filtered white noise. Metrologia 45 S117–S126.
LinkOut - more resources
Full Text Sources

