A utility approach to individualized optimal dose selection using biomarkers
- PMID: 31692022
- PMCID: PMC9011407
- DOI: 10.1002/bimj.201900030
A utility approach to individualized optimal dose selection using biomarkers
Abstract
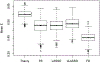
In many settings, including oncology, increasing the dose of treatment results in both increased efficacy and toxicity. With the increasing availability of validated biomarkers and prediction models, there is the potential for individualized dosing based on patient specific factors. We consider the setting where there is an existing dataset of patients treated with heterogenous doses and including binary efficacy and toxicity outcomes and patient factors such as clinical features and biomarkers. The goal is to analyze the data to estimate an optimal dose for each (future) patient based on their clinical features and biomarkers. We propose an optimal individualized dose finding rule by maximizing utility functions for individual patients while limiting the rate of toxicity. The utility is defined as a weighted combination of efficacy and toxicity probabilities. This approach maximizes overall efficacy at a prespecified constraint on overall toxicity. We model the binary efficacy and toxicity outcomes using logistic regression with dose, biomarkers and dose-biomarker interactions. To incorporate the large number of potential parameters, we use the LASSO method. We additionally constrain the dose effect to be non-negative for both efficacy and toxicity for all patients. Simulation studies show that the utility approach combined with any of the modeling methods can improve efficacy without increasing toxicity relative to fixed dosing. The proposed methods are illustrated using a dataset of patients with lung cancer treated with radiation therapy.
Keywords: constrained LASSO; efficacy toxicity trade-off; optimal treatment regime; personalized medicine; utility.
© 2019 WILEY-VCH Verlag GmbH & Co. KGaA, Weinheim.
Conflict of interest statement
Conflict of Interest
The authors have declared no conflict of interest.
Figures
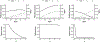
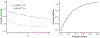
Similar articles
-
Utility based approach in individualized optimal dose selection using machine learning methods.Stat Med. 2022 Jul 20;41(16):2957-2977. doi: 10.1002/sim.9396. Epub 2022 Mar 28. Stat Med. 2022. PMID: 35343595 Free PMC article.
-
Personalized dose selection in radiation therapy using statistical models for toxicity and efficacy with dose and biomarkers as covariates.Stat Med. 2014 Dec 30;33(30):5330-9. doi: 10.1002/sim.6285. Epub 2014 Aug 27. Stat Med. 2014. PMID: 25164860 Free PMC article.
-
A dose-finding approach for genomic patterns in phase I trials.J Biopharm Stat. 2020 Sep 2;30(5):834-853. doi: 10.1080/10543406.2020.1744619. Epub 2020 Apr 20. J Biopharm Stat. 2020. PMID: 32310707
-
[The molecular markers related to personalized therapy of non-small cell lung cancer].Zhongguo Fei Ai Za Zhi. 2011 Mar;14(3):292-6. doi: 10.3779/j.issn.1009-3419.2011.03.17. Zhongguo Fei Ai Za Zhi. 2011. PMID: 21426677 Free PMC article. Review. Chinese. No abstract available.
-
Individualized therapy in non-small-cell lung cancer: future versus current clinical practice.Oncogene. 2009 Aug;28 Suppl 1:S38-45. doi: 10.1038/onc.2009.200. Oncogene. 2009. PMID: 19680295 Review.
Cited by
-
Utility based approach in individualized optimal dose selection using machine learning methods.Stat Med. 2022 Jul 20;41(16):2957-2977. doi: 10.1002/sim.9396. Epub 2022 Mar 28. Stat Med. 2022. PMID: 35343595 Free PMC article.
-
Direct incorporation of patient-specific efficacy and toxicity estimates in radiation therapy plan optimization.Med Phys. 2022 Oct;49(10):6279-6292. doi: 10.1002/mp.15940. Epub 2022 Sep 2. Med Phys. 2022. PMID: 35994026 Free PMC article.
References
-
- He T (2011). Lasso and general L1-regularized regression under linear equality and inequality constraints. Unpublished Ph.D. thesis, Purdue University, Dept. of Statistics.
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources

