SAD phasing of XFEL data depends critically on the error model

Abstract

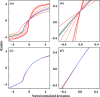
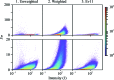
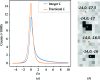
A nonlinear least-squares method for refining a parametric expression describing the estimated errors of reflection intensities in serial crystallographic (SX) data is presented. This approach, which is similar to that used in the rotation method of crystallographic data collection at synchrotrons, propagates error estimates from photon-counting statistics to the merged data. Here, it is demonstrated that the application of this approach to SX data provides better SAD phasing ability, enabling the autobuilding of a protein structure that had previously failed to be built. Estimating the error in the merged reflection intensities requires the understanding and propagation of all of the sources of error arising from the measurements. One type of error, which is well understood, is the counting error introduced when the detector counts X-ray photons. Thus, if other types of random errors (such as readout noise) as well as uncertainties in systematic corrections (such as from X-ray attenuation) are completely understood, they can be propagated along with the counting error, as appropriate. In practice, most software packages propagate as much error as they know how to model and then include error-adjustment terms that scale the error estimates until they explain the variance among the measurements. If this is performed carefully, then during SAD phasing likelihood-based approaches can make optimal use of these error estimates, increasing the chance of a successful structure solution. In serial crystallography, SAD phasing has remained challenging, with the few examples of de novo protein structure solution each requiring many thousands of diffraction patterns. Here, the effects of different methods of treating the error estimates are estimated and it is shown that using a parametric approach that includes terms proportional to the known experimental uncertainty, the reflection intensity and the squared reflection intensity to improve the error estimates can allow SAD phasing even from weak zinc anomalous signal.

Keywords: SAD phasing; XFELs; cctbx.xfel; error modeling; serial crystallography.

Figure 1

Normal probability plots for 5000 images. A 5000-image subset of the data was merged using protocol 3. During each step of the parameter refinement, a normal probability plot was generated (a). The rankits (equation 12) are plotted versus the sorted normalized deviations from the mean (equation 11). Each line represents one step during refinement and is colored using a rainbow color map from red (early steps) to blue (late steps). This is a non-gain-corrected data set. (b) Enlargement of the central area of (a) used to compute the slope and offset for initialization of the parameters. (c) As (a) but with a gain-corrected data set, in which each pixel was divided by 25. (d) As (b) for the central area of (c).

Figure 2

Intensity and σ versus resolution. 2D histograms of I, σ and I/σ (top, middle and bottom) versus resolution for the three error models. Data are for merged values. Note that the y axes and the color are on a logarithmic scale.

Figure 3

I/σ versus I plots with different error models. 2D histograms of I/σ versus I for the three error models. Unmerged intensities and error estimates are shown. In the top and bottom plots the same data are presented but with different scales for the y axis. Note that the color is on a logarithmic scale.

Figure 4

Histogram of I/σ for signal versus noise. (a) A random subset of 3800 images from one processing run of thermolysin was re-integrated, including the prediction of non-existent reflections at the halfway positions along the c* axis. These predictions, which are halfway between observed reflections, are composed of only noise. (b) Example of reflections labeled with integer L and fractional L indices.

Figure 5

Effect of image count on autobuilding success. For each of the three protocols, increasing numbers of images were processed. The anomalous peak height for the Zn²⁺ atom (a), the number of heavy-atom sites found (out of six) (b), the known model-to-map CC (c) and the number of residues built (d) are shown versus the number of images in the data set. In each case, shaded areas indicate the standard deviation of either the ten subsamples (data sets 1000–100 000) or the ten random seeds (full data set, 164 063 images). Note that for (b) certain data points have the same number of sites found in all trials and hence have no standard deviation.