Hybrid classical-quantum linear solver using Noisy Intermediate-Scale Quantum machines

Abstract

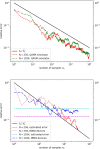
We propose a realistic hybrid classical-quantum linear solver to solve systems of linear equations of a specific type, and demonstrate its feasibility with Qiskit on IBM Q systems. This algorithm makes use of quantum random walk that runs in [Formula: see text](N log(N)) time on a quantum circuit made of [Formula: see text](log(N)) qubits. The input and output are classical data, and so can be easily accessed. It is robust against noise, and ready for implementation in applications such as machine learning.

Figure 1

(a) Quantum (or classical) random walk on an undirected $N=4$ graph. The transition probability of going from node $I$ to node $J$ or vice versa is equal to $P_{I,J}$, these elements forming a $4\times 4$ matrix. (b) The four nodes on this Hamming cube are labeled by integers $(0,1,2,3)$; they are encoded as four different states $\mathrm{|00}\rangle$, $\mathrm{|01}\rangle$, $\mathrm{|10}\rangle$, $\mathrm{|11}\rangle$, respectively.

Figure 2

Discrete-time coined quantum walk circuit for the $4\times 4$ transition matrix given in Eq. (10). Qubits $j_0$ and $j_1$ are state register qubits to represent the four-node graph in Fig. 1, first set as 0 before initialization, while the qubit $j_2$ is the coin register qubit. The measured registers $c_0$ and $c_1$ are fed back to initialize the next iteration. The classical-step is repeated c times to obtain the Neumann expansion up to order c.

Figure 3

Relative errors $\epsilon =|x_I^{exact}-x_I|/|x_I^{exact}|$ as a function of the sampling number n_s for $N=256$ and $N=1024$ matrices. The relevant parameters and estimated errors for these two matrices can be found in Table 1. Black solid lines represent the $\mathrm{1/}\sqrt{n_s}$ error reduction expected for Monte Carlo calculations. (Upper figure) Red dashed line and green dash-dotted line are the results computed by the QASM simulator. (Lower figure) Blue dash-dotted line and red dotted line are data for the same matrices computed by the IBM Q 20 Tokyo machine or Poughkeepsie machine. Cyan and magenta horizontal dashed lines depict the estimated errors.

Figure 4

Relative errors $\epsilon =|x_I^{exact}-x_I|/|x_I^{exact}|$ as a function of the sampling number n_s for $N=64$ and $N=128$ matrices, obtained by performing two quantum walk evolutions, ${\mathcal{U}}^2$. Black solid lines represent the $1/\sqrt{n_s}$ error reduction expected for Monte Carlo calculations. Red dashed line and blue dotted line are the results computed by the QASM simulator.