Frequency cluster formation and slow oscillations in neural populations with plasticity

Abstract

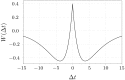
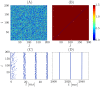
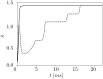
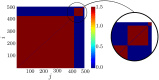
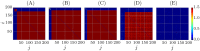
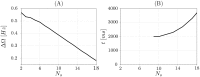
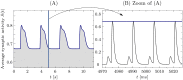
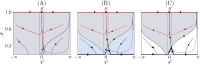
We report the phenomenon of frequency clustering in a network of Hodgkin-Huxley neurons with spike timing-dependent plasticity. The clustering leads to a splitting of a neural population into a few groups synchronized at different frequencies. In this regime, the amplitude of the mean field undergoes low-frequency modulations, which may contribute to the mechanism of the emergence of slow oscillations of neural activity observed in spectral power of local field potentials or electroencephalographic signals at high frequencies. In addition to numerical simulations of such multi-clusters, we investigate the mechanisms of the observed phenomena using the simplest case of two clusters. In particular, we propose a phenomenological model which describes the dynamics of two clusters taking into account the adaptation of coupling weights. We also determine the set of plasticity functions (update rules), which lead to multi-clustering.

Fig 1. Plasticity function W(Δt_ij) for τ_p = 2, τ_d = 5, c_p = 2, c_d = 1.6.

Fig 2. Synchronization into one Cluster.

Evolution of the coupling matrix κ_ij(t) starting from random initial conditions and converging to a completely synchronous state. Panel (A) shows initial coupling matrix, (B) the coupling matrix after the transient t = 2000ms. Raster plot of spiking times at the beginning of simulations (C) and after the transient (D). The asymptotic state (B,D) is a completely synchronized spiking with all coupling weights κ_ij potentiated to k_max. Other parameters N = 200, τ_p = 2, τ_d = 5, c_p = 2, c_d = 1.6, and κ_max = 1.5.

Fig 3. Frequency clusters.

Evolution of the coupling matrix κ_ij(t) starting from random initial conditions and converging to frequency clusters hierarchical in size. Panel (A) shows initial coupling matrix, (B) the coupling matrix after the transient t = 5600ms, and (C) t = 20000ms. (B-F) Corresponding raster plots of spike times. The asymptotic state (C,F) is a hierarchical cluster state with the coupling weights κ_ij potentiated to k_max within each cluster and small or zero otherwise. Other parameters as in Fig 2. The oscillators are ordered accordingly to their mean frequency.

Fig 4. Cluster formation.

Formation of individual clusters over time (corresponds to the dynamical scenario in Fig 3). The dashed and solid curves depict the time course of the mean coupling within the small and big clusters, respectively.

Fig 5. Three-cluster state.

Example of a three-cluster state for N = 500, τ_p = 2, τ_d = 5, c_p = 2, c_d = 1.6, and κ_max = 1.5 with a random initial distribution of κ_ij in [0, 0.75].

Fig 6. Influence of independent random input on clusters.

Coupling matrices for t = 10000ms and different amplitudes of independent random input I (see Eq (4)). (A) I = 0.005, (B) I = 0.01, (C) I = 0.02, (D) I = 0.05 and (E) I = 0.07. All other parameters as in Fig 5.

Fig 7. Cluster frequencies and time until fusion.

(A)Difference between synchronization frequencies of the two clusters for different size of the smaller cluster N_s. (B) Time until cluster fusion for different initial size of the smaller cluster N_s.

Fig 8. Two cases: Fusion and stable clusters.

Evolution of the coupling matrix for N = 50 and the number of neurons N_s = 8 (A)-(C) and N_s = 9 (D)-(F) in the small cluster. In panels (A)-(C) the clusters are stable, while in (D)-(F) they are merging to one synchronous cluster. (G, H) Time courses of the spiking synchronization frequencies of small (N_s neurons) and large (N_b neurons) clusters depicted by dashed and solid curves, respectively, for (G) N_s = 8 and N_b = 42 and (H) N_s = 9 and N_b = 41. Parameter κ_max = 1.0.

Fig 9. Mean synaptic activity.

Mean synaptic activity S(t) of the neural population in the case of stable two cluster state. Panel (A) shows the dynamics of S(t) on the time interval of 12 s, where modulation of the amplitude (blue line) is visible, while the fast oscillations are not recognized on this timescale. The maximum amplitude corresponds to the two clusters being synchronised, while the low amplitude corresponds to the clusters being out of phase. Panel (B) shows the zoom of a small time interval. The modulation takes place on the timescale which is two orders of magnitude larger than the individual spikes of S(t) as well as individual neural spikes in both clusters. Cluster frequencies ω₁ = 0.065012 kHz and ω₂ = 0.065416 kHz. The corresponding period of modulation is T ≈ 2.5s.

Fig 10. Update function G.

(A) Update function G(φ) for τ_p = 2, τ_d = 5, c_p = 2, and c_d = 1.6. (B) Schematic spiking of two oscillators with spike time difference ΔT and periods close to T.

Fig 11. Phase portrait phenomenological model.

Phase portraits of model (10)–(11) for (A) monostable regime of complete synchronization; (B) co-existence of stable synchronized and clustered states; and (C) bifurcation moment of transition between the phase portraits illustrated in (A) and (B). The basins of attraction of the synchronized regime (point S), clustered state (limit cycle indicated by thick black curve) and the saddle fixed point (φ*, σ*) are depicted by gray, blue, and white colors, respectively. The nullclines of the system and stable and unstable manifolds of the saddle point are indicted by the thin gray and black curves, respectively. Parameters (A) ω = 0.037 kHz, (B) ω = 0.06 kHz, (C) ω ≈ 0.455 Hz, and the other parameters τ_p = 2, τ_d = 5, c_p = 2, c_d = 1.6, and ε = 0.08.

Fig 12. Phase portrait Hodgkin-Huxley model.

Dynamics of the phase difference between the clusters φ_HH and mean inter-cluster coupling σ_HH for the solutions of the HH system (1)–(3) for different initial conditions. N = 50 with N_s = 7 neurons in the small cluster and N_b = 43 in the big one. Red orbits converge to the regime of complete synchronization, and blue trajectories lead to a stable two-cluster solutions. The nullclines of the phenomenological model are shown in gray. Other parameters: τ_p = 2, τ_d = 5, c_p = 2, c_d = 1.6, and κ_max = 1.5.

Fig 13. Parameter (c_p, c_d)-plane of the plasticity function.

Panel (A): system (10)–(11). White region: stable periodic solution coexisting with a stable fixed point, case II. Black region: globally stable fixed point, case I. Grey region: globally stable periodic solution with σ = 0. Panel (B): original system (1)–(3). White: stable two-clusters (white); black: stable synchrony and no stable clusters; grey: decoupling of all neurons. Other parameters τ_p = 2, τ_d = 5, N = 50, N_s = 7, and κ_max = 1.