The 'breakpoint' of soil-transmitted helminths with infected human migration

Abstract

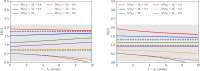
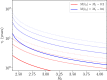
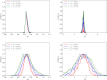
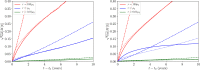
Building on past research, we here develop an analytic framework for describing the dynamics of the transmission of soil-transmitted helminth (STH) parasitic infections near the transmission breakpoint and equilibria of endemic infection and disease extinction, while allowing for perturbations in the infectious reservoir of the parasite within a defined location. This perturbation provides a model for the effect of infected human movement between villages with differing degrees of parasite control induced by mass drug administration (MDA). Analysing the dynamical behaviour around the unstable equilibrium, known as the transmission 'breakpoint', we illustrate how slowly-varying the dynamics are and develop an understanding of how discrete 'pulses' in the release of transmission stages (eggs or larvae, depending on the species of STH), due to infected human migration between villages, can lead to perturbations in the deterministic transmission dynamics. Such perturbations are found to have the potential to undermine targets for parasite elimination as a result of MDA and/or improvements in water and sanitation provision. We extend our analysis by developing a simple stochastic model and analytically investigate the uncertainty this induces in the dynamics. Where appropriate, all analytical results are supported by numerical analyses.

Keywords: Control policies; Mathematical models; Monitoring and evaluation; Soil-transmitted helminths; Transmission breakpoints.

Fig. 1

A visualisation of the phase plane generated by Eq. (6) (with $k=0.3$ and $\gamma =0.08$) where black solid and dashed lines correspond to the two branches of equilibrium solution numerically obtained by satisfying Eq. (9). In both panels the heatmap corresponds to the strength and direction of the first derivatives M′(t) (and second, up to a negative constant $-(\mu +{\mu }_1)M^{\prime }\left(t\right)$ — see Eq. (8)) computed through Eq. (6) in the vertical direction (lines of constant R₀), where lighter colours correspond to strongly positive values (strong forces upwards) and darker colours correspond to strongly negative values (strong forces downwards) — consequently, intermediate colours have the weakest forces in either direction. The right panel is a zoomed version of the left panel with enhanced colour contrast for illustration purposes. The increasing timescales to travel between distances of, e.g., $M=[1.0\to 1.1,0.9\to 1.0,0.83\to 0.9]$ for a fixed value of $R_0=2.12$ are $t-t_0\simeq [9.6\text{years},12.9\text{years},23.4\text{years}]$.

Fig. 2

The approximative solution to the transmission dynamics given in Eq. (18) against the full solution to the dynamics obtained numerically by solving the equivalent system with Eqs. (1) and (2), each represented by the coloured solid and dashed lines, respectively, for a range of initial conditions M(t₀). In the left panel we have fixed a value of $R_0=R_{0†}(z,k)+0.1\simeq 2.18$ and in the right panel with a value of $R_0=R_{0†}(z,k)+0.01\simeq 2.09$. The dotted black horizontal lines corresponds to the value of M at the stable (upper) and unstable (lower) equilibria numerically obtained from Eq. (9). Lastly, the grey region corresponds to values for which $|M-M_{†}(z,k)|<1$ and hence the expansion used to obtain Eq. (18) leads to good agreement with the full numerical solution.

Fig. 3

Numerically-obtained values using integral in Eq. (21) to compute the length of time it takes for the transmission dynamics to reach the value of $M=M_{†}(z,k)$ for two different initial values of $M=M\left(t_0\right),$ as shown in the legend. A range of worm death rates have been used of ${\mu }_1=1/2{\text{years}}^{-1},1/5{\text{years}}^{-1},1/8{\text{years}}^{-1},1/12{\text{years}}^{-1}$ in decreasing order, which corresponds to a fading colour in the plotted lines.

Fig. 4

The approximative solution to the transmission dynamics given in Eq. (23) (applied where we have set $t_{\text{pul}}=2\text{years}$ and Eq. (18) as the solution to the dynamics before this point) against the full solution to the dynamics obtained numerically by solving the equivalent system with Eqs. (1) and (2), each represented by the coloured solid and dashed lines, respectively, for a range of initial conditions M(t₀). All lines and the grey region correspond to their equivalent values in Fig. 2, where an additional upper and lower panel split in this set of figures compares the relative dynamical behaviour under the influence of a migration perturbation of $\beta \delta L\left(t_{\text{pul}}\right)=+1(-1){\text{years}}^{-1}$ for the upper (lower) pair of panels.

Fig. 5

The approximative solution to the transmission dynamics given in Eq. (26) against the full solution to the dynamics obtained numerically by solving the equivalent system with Eqs. (1) and (2), each represented by the coloured solid and dashed lines, respectively, for a range of initial conditions M(t₀) and having fixed a value of $R_0=R_{0†}(z,k)+1.0\simeq 3.08$. In the left panel we plot the transmission dynamics around the stable equilibrium, and in the right panel we plot the dynamics around the unstable equilibrium. The solid black horizontal line corresponds to the value of $M=M_{*}(z,k,R_0)$ at the stable (left panel) and unstable (right panel) equilibrium numerically obtained from Eq. (9). Lastly, the grey region corresponds to values for which $|M-M_{*}(z,k,R_0)|<1$.

Fig. 6

A comparison between the probability distributions P(M, t) at different snaphots in time (denoted by different colours) using $r=0.1{\mu }_2$ (top panels) and $r=10{\mu }_2$ (bottom panels) migration rates, having initialised $P(M,t_0)={\delta }_{\mathrm{D}}(M_{*}-M)$ (where δ_D is a Dirac delta function) at the unstable (left column) and stable (right column) equilibrium points M_*, given a choice of $R_0=R_{0†}(z,k)+0.1\simeq 2.18$. The solid lines indicate that the fully non-Markovian process given by Eq. (36) is used, whereas the dashed lines indicate the corresponding choice of approximate Markovian process, given by Eq. (37). The distributions themselves have been numerically obtained by binning 10³ realisations of Eq. (40).

Fig. 7

The root-variance over M(t) initialised at the unstable equilibrium M_* value (left panel) and at the stable equilibrium M_* value (right panel), plotted as a function of time, and numerically obtained by summing over 10³ realisations of Eq. (40) using the non-Markovian (solid coloured lines) and Markovian (dotted coloured lines) migration processes given by Eqs. (36) and (37), respectively. The dashed coloured lines correspond to the analytic Markovian solution given in Eq. (41).