The Demands of Geometry on Color Vision

Abstract

While studies of human color vision have made enormous strides, an overarching rationale for the circular sense of color relationships generated by two classes of color opponent neurons and three cone types is still lacking. Here we suggest that color circularity, color opponency and trichromacy may have arisen, at least in part, because of the geometrical requirements needed to unambiguously distinguish all possible spectrally different regions on a plane.

Keywords: color circularity; four-color map problem; opponency; perception; spectral images; trichromacy; unique hues.

Figure 1

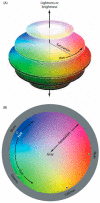
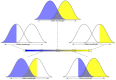
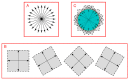
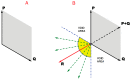
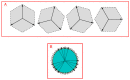
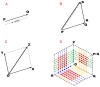
Diagram of human color perception. (A) A representation of human “color space”; (B) A single cross-sectional plane from the diagram in (A). When asked to arrange a large number of equiluminant surfaces that vary in hue such that the color differences among them are minimal, subjects arrange them in a closed loop that comprises four basic color categories (reds, greens, blues and yellows), each defined by a particular hue (black dots) that has no admixture of the neighboring color classes (e.g., a red surface seen as having no appreciable yellowness or blueness). Although there are many other named color groups (oranges, aquamarines, etc.), these are always seen as mixtures of the two of the four primaries. As indicated, the location of the unique hues (black dots) are not orthogonal in perceptual color space, nor is the closed loop determined psychophysically a literal circle as shown in the diagram.

Figure 2

Distinguishing neighboring regions in one dimension. (A) Two different qualities (blue and yellow in this example) suffice to distinguish any number of neighboring regions from one another along a line; (B) However, a continuum is needed when points must be distinguished according to relative spectral differences at equiluminance. Notice that the balance point in a color continuum would be perceived is neither one color nor the other (i.e., neither blue nor yellow but a shade of gray).

Figure 3

Color specification in 1D achieved by two opposing photoreceptor types. Top panel. Hypothetical cone sensitivity curves. When stimulated equally, the perceptual result would be color neutrality. Middle panels. When the response of one of the photoreceptor types is maximal and the other minimal, the perception would be that of unique blue (left) or unique yellow (right). Bottom panel. Stimulation that would give rise to predominantly blue (left) or yellow (right) perceptions along the color continuum in Figure 2B.

Figure 4

Distinguishing different spectral regions in a two-dimensional image. (A) A two-dimensional vector space extends in all directions from its null point; (B) Vector addition based on any two axes in the plane defines position vectors in all directions (four of the many arrangements possible are shown as examples); (C) The position vectors held in common by the full set of direction vectors would be necessarily be bounded by a closed loop, as indicated by the area in green. Notice that the loop would form a circle only if the vectors were all the same length, which the argument here does not require.

Figure 5

The four-color demand for regional distinctions on a map and the color opponency that would be needed. (A) The demand in 2D geometry refers to the fact that abutting regions on a plane cannot be distinguished using fewer than four colors. The diagram shows a simple example which makes clear that these regions could not be distinguished from one another using fewer than four colors. If this pattern were an equiluminant retinal image, the four regions would need to elicit color sensations that could distinguish any possible hue within these four color classes (reds, greens, blues and yellows); (B) Two opposing color quality pairs (direction vectors) extending from a null point (white dot) would be sufficient to address this issue, at the same time as differentiating all points (position vectors) on a plane by a gamut of color sensations. Note that the opponent axes would not have to be orthogonal.

Figure 6

How three direction vectors can specify all possible locations (position vectors) on a plane. (A) Two non-opposing direction vectors (P and Q) could, by vector addition, specify all the position vectors that lie between them (the gray parallelogram); (B) A third direction vector, if appropriately positioned, would allow the resulting triad of vectors (P, Q and R) to specify locations in all directions. To deal with the four-color map demand, however, the third direction vector would have to oppose the combined influence of other two direction vectors, i.e., vector P + Q indicated by the dashed black line.

Figure 7

A closed 2D space defined by three direction vectors. (A) Vector addition based on three direction vectors placed appropriately (see Figure 6) would define position vectors in all directions on a plane (only four of many possible arrangements are shown as examples); (B) The position vectors held in common by the full set of such direction vectors form a circular space (green area) in this example.

Figure 8

Using vector addition to describe spectral images. (A) PQ represents a vector directed from point P to point Q, the initial and terminal points of the vector. The magnitude of PQ thus indicates “x” units acting in that direction; (B) The tip-to-tail method vector addition, showing how PS is generated from vectors PQ and RS; (C) Addition of vectors OX and OY using the parallelogram law of vector addition; (D) A 2D vector space with point O as origin. The green, yellow, and blue dots represent the end points (position vectors) of the direction vectors P, Q and, respectively. The red dots end points of position vectors determined as vector sums of the position vectors corresponding dotted lines.