Observation of quantum many-body effects due to zero point fluctuations in superconducting circuits

Abstract

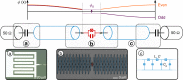
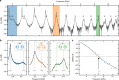
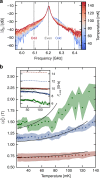
Electromagnetic fields possess zero point fluctuations which lead to observable effects such as the Lamb shift and the Casimir effect. In the traditional quantum optics domain, these corrections remain perturbative due to the smallness of the fine structure constant. To provide a direct observation of non-perturbative effects driven by zero point fluctuations in an open quantum system we wire a highly non-linear Josephson junction to a high impedance transmission line, allowing large phase fluctuations across the junction. Consequently, the resonance of the former acquires a relative frequency shift that is orders of magnitude larger than for natural atoms. Detailed modeling confirms that this renormalization is non-linear and quantum. Remarkably, the junction transfers its non-linearity to about thirty environmental modes, a striking back-action effect that transcends the standard Caldeira-Leggett paradigm. This work opens many exciting prospects for longstanding quests such as the tailoring of many-body Hamiltonians in the strongly non-linear regime, the observation of Bloch oscillations, or the development of high-impedance qubits.

Fig. 1

SQUID chains coupled to a small Josephson junction (weak link). The upper part represents the spatial phase distribution of the two first standing waves or resonant modes of the total system (Josephson junction + chains). And odd (even) mode—which couples (does not couple) to the junction—is represented in purple (orange). The lower part is a schematic of the system. The SQUID chains, depicted as blue transmission lines, are capacitively coupled to the input and output 50 Ω coaxial cables and galvanically coupled to the small Josephson junction (in red). a Optical picture of the input and output capacitive couplings. b SEM picture of a few of the SQUIDs (1500 in total for each chain) that are coupled to the small Josephson junction (in red). c Equivalence between the transmission line effective picture and the SQUID chain characterized by three microscopic parameters $L$ and $C$ the inductance and capacitance per SQUID respectively and $C_g$ the ground capacitance

Fig. 2

Inferring the renormalized resonant frequency ${\omega }_{\mathrm{J}}^{*}$ of the small Josephson junction. a Amplitude of the microwave transmission $\mid S_{21}\mid$ versus frequency (sample A, 24 mK). The even–odd modes frequency splitting $S$ changes sign precisely at ${\omega }_{\mathrm{J}}^{*}$. Arrows are guides to the eye of the splitting sign. b Fit of the double peaks for three cases: well below the resonant frequency of the small Josephson junction (blue) its inductive part dominates, close to ${\omega }_{\mathrm{J}}^{*}$ (orange) the impedance of the junction is large so that the two modes are almost decoupled, and well above ${\omega }_{\mathrm{J}}^{*}$ (green) the capacitive part of the junction dominates. c Experimental normalized frequency splittings $S$ obtained from the previous fits (dots) and theoretical prediction (full line). The resonance frequency ${\omega }_{\mathrm{J}}^{*}$ of the small Josephson junction corresponds to the vanishing value of the normalized splitting $S$

Fig. 3

Temperature-induced renormalization. a Zoom on a even–odd pair of transmission peaks for sample A at temperature ranging from 23 to 150 mK. The even mode (gray) does not move while the odd mode (blue is at 25 mK, red at 130 mK) shifts down in frequency when warming up, showing a downward renormalization of the junction frequency ${\omega }_{\mathrm{J}}^{*}$. b ZPF of the small junction $⟨{\varphi }_{\mathrm{J}}^2⟩$ as a function of the temperature for three samples (A, B, and C ranging from dark to light blue), extracted from Eq. (2). ZPF are stronger in sample A, which is associated to a smaller ratio $E_{\mathrm{J,bare}}∕E_{\mathrm{c}}$ (large nonlinearity). The measured quantum to classical crossover is in good agreement with theory (full lines). The inset displays the corresponding renormalized junction frequency $f_{\mathrm{J}}^{*}={\omega }_{\mathrm{J}}^{*}∕2\pi$ of the three samples. The full lines are the SCHA predictions while the dashed lines represent what would be the temperature evolution of these frequencies if ZPF were omitted from $⟨{\varphi }_{\mathrm{J}}^2⟩$, using the same values of $E_{\mathrm{J,bare}}$

Fig. 4

Many-body nature of the ZPF. Total phase fluctuations across the small Josephson junction in sample B, taking into account in our model (full lines) different numbers of modes of the environment, ranging from one (light blue) to the total number (dark blue). The inset shows the relative contribution of the different modes to the total fluctuations, with ${\mathrm{\Gamma }}_{\mathrm{J}}$ being the FWHM of this quantity