Mechanical power at a glance: a simple surrogate for volume-controlled ventilation

Abstract

Background: Mechanical power is a summary variable including all the components which can possibly cause VILI (pressures, volume, flow, respiratory rate). Since the complexity of its mathematical computation is one of the major factors that delay its clinical use, we propose here a simple and easy to remember equation to estimate mechanical power under volume-controlled ventilation: [Formula: see text] where the mechanical power is expressed in Joules/minute, the minute ventilation (VE) in liters/minute, the inspiratory flow (F) in liters/minute, and peak pressure and positive end-expiratory pressure (PEEP) in centimeter of water. All the components of this equation are continuously displayed by any ventilator under volume-controlled ventilation without the need for clinician intervention. To test the accuracy of this new equation, we compared it with the reference formula of mechanical power that we proposed for volume-controlled ventilation in the past. The comparisons were made in a cohort of mechanically ventilated pigs (485 observations) and in a cohort of ICU patients (265 observations).

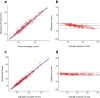
Results: Both in pigs and in ICU patients, the correlation between our equation and the reference one was close to the identity. Indeed, the R² ranged from 0.97 to 0.99 and the Bland-Altman showed small biases (ranging from + 0.35 to - 0.53 J/min) and proportional errors (ranging from + 0.02 to - 0.05).

Conclusions: Our new equation of mechanical power for volume-controlled ventilation represents a simple and accurate alternative to the more complex ones available to date. This equation does not need any clinical intervention on the ventilator (such as an inspiratory hold) and could be easily implemented in the software of any ventilator in volume-controlled mode. This would allow the clinician to have an estimation of mechanical power at a simple glance and thus increase the clinical consciousness of this variable which is still far from being used at the bedside. Our equation carries the same limitations of all other formulas of mechanical power, the most important of which, as far as it concerns VILI prevention, are the lack of normalization and its application to the whole respiratory system (including the chest wall) and not only to the lung parenchyma.

Keywords: Mathematical computation; Mechanical power; Pressure-controlled ventilation; Volume-controlled ventilation.

Fig. 1

Mechanical power equations for volume-controlled and pressure-controlled ventilation. Six equations for the calculation of mechanical power are available to date. For volume-controlled ventilation, the extended equation proposed by Gattinoni et al. still represents the reference equation and the simplified equation proposed by the same group is a mathematical rearrangement of it, which means that the two formulas can be considered identical. The surrogate equation that we propose in this paper carries a small bias (underestimation), but also the advantage of being simple and easily available just by looking at the ventilator. For pressure-controlled ventilation, the two extended equations proposed by Van der Meijden et al. and by Becher et al. are both very accurate, but complex. As for our surrogate, the one proposed by Becher et al. carries a small bias (overestimation), but also the advantage of being simple and easily available just by looking at the ventilator

Fig. 2

Geometrical view of mechanical power for volume-controlled ventilation. Left pane (a) l: the violet contoured trapezoid represents the mechanical power as calculated with the reference formula (Eq. 1). Right panel  (b): the violet contoured trapezoid represents the mechanical power as calculated with our unadjusted surrogate (Eq. 3). The violet-filled triangle represents the bias (Eq. 4) between our unadjusted surrogate (Eq. 3) and the reference formula (Eq. 1)

Fig. 3

a, b: Relationship between our unadjusted surrogate of mechanical power (Eq. 3) and the reference formula (Eq. 1) in pigs: panel a shows the linear regression (R² = 0.98), and panel b shows the Bland-Altman (bias = − 2.45 J/min; proportional error = − 0.09 J/min). c, d Relationship between our adjusted surrogate of mechanical power (Eq. 9) and the reference formula (Eq. 1) in pigs: panel c shows the linear regression (R² = 0.99), and panel d shows the Bland-Altman (bias = 0.21 J/min; proportional error = 0.01 J/min)

Fig. 4

a, b Relationship between our unadjusted surrogate of mechanical power (Eq. 3) and the reference formula (Eq. 1) in ICU patients treated with 5 cmH₂O of PEEP: panel a shows the linear regression (R² = 0.96), and panel b shows the Bland-Altman (bias = − 3.43 J/min; proportional error = − 0.27 J/min). c, d Relationship between our adjusted surrogate of mechanical power (Eq. 9) and the reference formula (Eq. 1) in ICU patients treated with 5 cmH₂O of PEEP: panel c shows the linear regression (R² = 0.98), and panel d shows the Bland-Altman (bias = − 0.53 J/min; proportional error = − 0.03 J/min)

Fig. 5

a, b Relationship between our unadjusted surrogate of mechanical power (Eq. 3) and the reference formula (Eq. 1) in ICU patients treated with 15 cmH₂O of PEEP: panel a shows the linear regression (R² = 0.97), and panel b shows the Bland-Altman (bias = − 3.14 J/min; proportional error = − 0.21 J/min). c, d Relationship between our adjusted surrogate of mechanical power (Eq. 9) and the reference formula (Eq. 1) in ICU patients treated with 15 cmH₂O of PEEP: panel c shows the linear regression (R² = 0.97), and panel d shows the Bland-Altman (bias = − 0.28 J/min; proportional error = − 0.05 J/min). e, f Relationship between our adjusted surrogate of mechanical power (Eq. 3) and the reference formula (Eq. 1) in ICU patients treated with 15 cmH₂O of PEEP and with respiratory system resistances higher than 15 cmH₂O∙sec/liters: panel e shows the linear regression (R² = 0.98), and panel b shows the Bland-Altman (bias = − 1.35 J/min; proportional error = − 0.12 J/min)