Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2019 Dec;13(6):305-315.
doi: 10.1049/iet-syb.2019.0051.

Competitive numerical analysis for stochastic HIV/AIDS epidemic model in a two-sex population

Ali Raza  1 , Muhammad Rafiq  2 , Dumitru Baleanu  3 , Muhammad Shoaib Arif  4 , Muhammad Naveed  4 , Kaleem Ashraf  5
Affiliations

Competitive numerical analysis for stochastic HIV/AIDS epidemic model in a two-sex population

Ali Raza et al. IET Syst Biol. 2019 Dec.

Abstract

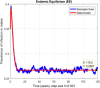
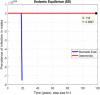
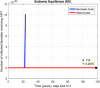
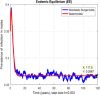
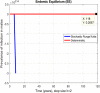
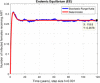
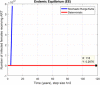
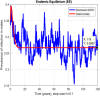
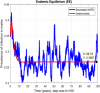
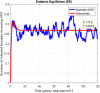
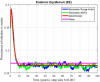
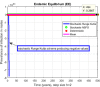
This study is an attempt to explain a reliable numerical analysis of a stochastic HIV/AIDS model in a two-sex population considering counselling and antiretroviral therapy (ART). The authors are comparing the solutions of the stochastic and deterministic HIV/AIDS epidemic model. Here, an endeavour has been made to explain the stochastic HIV/AIDS epidemic model is comparatively more pragmatic in contrast with the deterministic HIV/AIDS epidemic model. The effect of threshold number H* holds on the stochastic HIV/AIDS epidemic model. If H* < 1 then condition helps us to control disease in a two-sex human population while H* > 1 explains the persistence of disease in the two-sex human population. Lamentably, numerical methods such as Euler-Maruyama, stochastic Euler, and stochastic Runge-Kutta do not work for large time step sizes. The recommended structure preserving framework of the stochastic non-standard finite difference (SNSFD) scheme conserve all vital characteristics such as positivity, boundedness, and dynamical consistency defined by Mickens. The effectiveness of counselling and ART may control HIV/AIDS in a two-sex population.

PubMed Disclaimer

Figures

Fig. 1
Fig. 1
Flow diagram of the HIV/AIDS model in two sex populations
Fig. 2
Fig. 2
In the prevalence of infection in males stochastic Euler converges for h = 0.001
Fig. 3
Fig. 3
In the prevalence of infection in males, stochastic Euler shows negativity for h = 1
Fig. 4
Fig. 4
In a number of females receiving ART stochastic Euler converges for h = 0.001
Fig. 5
Fig. 5
In a number of females receiving ART stochastic Euler shows unboundedness for h = 1
Fig. 6
Fig. 6
In the prevalence of infection in males stochastic Runge Kutta converges for h = 0.001
Fig. 7
Fig. 7
In the prevalence of infection in males, stochastic Runge Kutta shows negativity for h = 2
Fig. 8
Fig. 8
In a number of females receiving ART stochastic Runge Kutta shows converges for h = 0.001
Fig. 9
Fig. 9
In a number of females receiving ART stochastic Runge Kutta shows unboundedness for h = 2
Fig. 10
Fig. 10
In the prevalence of infection in males stochastic NSFD converges for h = 0.01
Fig. 11
Fig. 11
In the prevalence of infection in males, stochastic NSFD converges for h = 100
Fig. 12
Fig. 12
In a number of females receiving ART stochastic NSFD converges for h = 0.1
Fig. 13
Fig. 13
In a number of females receiving ART stochastic NSFD converges for h = 100
Fig. 14
Fig. 14
Contrast of stochastic Euler, stochastic NSFD, deterministic and mean for h = 0.001
Fig. 15
Fig. 15
Contrast of stochastic Euler, stochastic NSFD, deterministic and mean for h = 0.9, but stochastic Euler shows negative values
Fig. 16
Fig. 16
Contrast of stochastic Runge–Kutta, stochastic NSFD, deterministic and mean for h = 0.001
Fig. 17
Fig. 17
Contrast of stochastic Runge–Kutta, stochastic NSFD, deterministic and mean for h = 2 but stochastic Runge Kutta shows negative values
See this image and copyright information in PMC

References

    1. Ochoche Jefrey M.: ‘Modeling HIV in the presence of infected immigrants and vertical transmission’, Int. J. Sci. Technol. Res., 2013, 2, (11), pp. 571–588
    1. Li Q. Cao S., and Chen X. et al.: ‘Stability analysis of an HIV dynamics model with drug resistance’, Discret. Dyn. Nat. Soc., 2012, 12, pp. 1530–1544
    1. Bhunu C.P. Mushayabasa S., and Kojouharov H. et al.: ‘Mathematical analysis of an HIV model impact of educational programs and abstinence in sub‐saharan Africa’, J. Math. Model Algorithms, 2011, 10, (1), pp. 31–55
    1. Kimbir A.R., and Oduwole H.K.: ‘A mathematical model of HIV transmission dynamics considering counselling and antiretroviral therapy’, J. Math. Stat. Model., 2008, 2, (5), pp. 166–169
    1. Hsieh Y.H.: ‘A two‐sex model for treatment of AIDS and behavior change in a population of varying size’, IMA J. Math. Appl. Biol. Sci., 1996, 13, (3), pp. 151–173 - PubMed

Substances