The first order statistics of backscatter from the fractal branching vasculature

Abstract

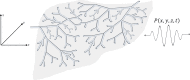
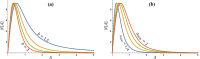
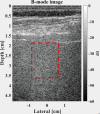
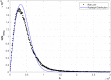
The issue of speckle statistics from ultrasound images of soft tissues such as the liver has a long and rich history. A number of theoretical distributions, some related to random scatterers or fades in optics and radar, have been formulated for pulse-echo interference patterns. This work proposes an alternative framework in which the dominant echoes are presumed to result from Born scattering from fluid-filled vessels that permeate the tissue parenchyma. These are modeled as a branching, fractal, self-similar, multiscale collection of cylindrical scatterers governed by a power law distribution relating to the number of branches at each radius. A deterministic accounting of the echo envelopes across the scales from small to large is undertaken, leading to a closed form theoretical formula for the histogram of the envelope of the echoes. The normalized histogram is found to be related to the classical Burr distribution, with the key power law parameter directly related to that of the number density of vessels vs diameter, frequently reported in the range of 2 to 4. Examples are given from liver scans to demonstrate the applicability of the theory.

FIG. 1.

(Color online) Model of 3D convolution of a pulse with the fractal branching cylindrical fluid-filled channels in a soft tissue.

FIG. 2.

(Color online) A cylindrical function (a) and its Hankel transform represented in 3D Fourier transform space (b). Rotations around spherical coordinates similarly rotate the corresponding transform. The transform of a propagating pulse is shown in (c). The maximum product of (b) and (c) arrives when the angle $\theta$ approaches zero.

FIG. 3.

(Color online) The RMS echo amplitude (vertical axis, arbitrary units) vs cylinder radius normalized by ${\sigma }_x$ from Eq. (6), and square root approximation, assuming a $G{H}_2$ pulse.

FIG. 4.

(Color online) The RMS echo amplitude for a second bandpass pulse shape with exponential tails vs normalized radius of a scattering cylinder, and a square root approximation.

FIG. 5.

(Color online) The proposed histogram function of envelope amplitudes $A$, having the form $A/{(A^2+a_{\text{min}})}^b$. In (a) are normalized functions where $a_{\text{min}}=1/2$ and the power law parameter $b$ is 3, 2.5, 2, and 1.5. In (b) are normalized functions where the power law parameter is fixed at 2.5; however, $a_{\text{min}}$ is varied as 1/4, 1/2, 3/4, and 1. Vertical axis: counts (arbitrary units); horizontal axis: envelope amplitude (arbitrary units).

FIG. 6.

(Color online) Left: ultrasound B-scan image from a 20 MHz scan of a normal rat liver, focused transmit at 11 mm depth. Right: zoom view of speckle region ROI selected for analysis.

FIG. 7.

(Color online) Histogram of echo amplitudes from the normal rat liver. Vertical axis = counts; horizontal axis = amplitudes of echo envelopes (arbitrary units). The dashed line indicates theoretical fit to the derived Eq. (10), with the power law parameter of $b=3.4$ and $\lambda =6.5\times {10}^5$.

FIG. 8.

(Color online) B-scan image of a healthy liver tissue in a human. A ROI is selected (dashed lines) for analysis.

FIG. 9.

(Color online) Data from a 5 MHz probe on a normal human liver with $b=2.9$ and $\lambda =3.3\times {10}^6$. Vertical axis: counts; horizontal axis: amplitudes of echo envelopes (arbitrary units).

FIG. 10.

(Color online) The comparison of the CDF of the rat liver echo amplitudes and the theoretical Burr distribution CDF.

FIG. 11.

(Color online) A comparison of the histogram of the rat liver echo amplitudes with a minimum mean squared error curve-fit to the classical Rayleigh distribution.

FIG. 12.

Schematic illustration following Papoulis showing the distribution of one continuous variable $x$ with a distribution $f_x(x)$ which is mapped to a new distribution where $y=g(x)$, and retaining the area under the curve.

FIG. 13.

(Color online) Example of sampling an envelope function (a) to produce a resulting histogram (b) and theory from Eq. (A1) (solid line). In (a), the vertical axis is amplitude, maximum value normalized to 1; the horizontal axis is time or distance, arbitrary units. In (b), the vertical axis is sampled counts in a histogram; the horizontal axis is echo amplitude. Note the spike near amplitude = 1, the local maximum of the envelope.

FIG. 14.

(Color online) Second example using a modified Gaussian envelope in (a) and the resulting histogram in (b), demonstrating the dominant value or singularity mapped from the local maximum. In (a), the vertical axis is amplitude, maximum value normalized to 1; the horizontal axis is time or distance, arbitrary units. In (b), the vertical axis is sampled counts in a histogram; the horizontal axis is echo amplitude. Note the spike near amplitude = 1, the local maximum of the envelope.