Tree-Weighting for Multi-Study Ensemble Learners
- PMID: 31797618
- PMCID: PMC6980320
Tree-Weighting for Multi-Study Ensemble Learners
Abstract
Multi-study learning uses multiple training studies, separately trains classifiers on each, and forms an ensemble with weights rewarding members with better cross-study prediction ability. This article considers novel weighting approaches for constructing tree-based ensemble learners in this setting. Using Random Forests as a single-study learner, we compare weighting each forest to form the ensemble, to extracting the individual trees trained by each Random Forest and weighting them directly. We find that incorporating multiple layers of ensembling in the training process by weighting trees increases the robustness of the resulting predictor. Furthermore, we explore how ensembling weights correspond to tree structure, to shed light on the features that determine whether weighting trees directly is advantageous. Finally, we apply our approach to genomic datasets and show that weighting trees improves upon the basic multi-study learning paradigm. Code and supplementary material are available at https://github.com/m-ramchandran/tree-weighting.
Figures
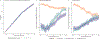
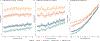

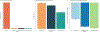
References
-
- Breiman L, Random forests, Machine Learning 45, 5 (October 2001).
-
- Breiman L, Bagging predictors, Machine Learning 24, 123 (August 1996).
-
- Maudes J, Rodŕíguez JJ, Garćía-Osorio C and Garćía-Pedrajas N, Random feature weights for decision tree ensemble construction, Inf. Fusion 13, 20 (January 2012).

