An empirical comparison of two novel transformation models

Abstract

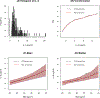
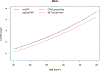
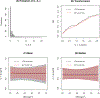
Continuous response variables are often transformed to meet modeling assumptions, but the choice of the transformation can be challenging. Two transformation models have recently been proposed: semiparametric cumulative probability models (CPMs) and parametric most likely transformation models (MLTs). Both approaches model the cumulative distribution function and require specifying a link function, which implicitly assumes that the responses follow a known distribution after some monotonic transformation. However, the two approaches estimate the transformation differently. With CPMs, an ordinal regression model is fit, which essentially treats each continuous response as a unique category and therefore nonparametrically estimates the transformation; CPMs are semiparametric linear transformation models. In contrast, with MLTs, the transformation is parameterized using flexible basis functions. Conditional expectations and quantiles are readily derived from both methods on the response variable's original scale. We compare the two methods with extensive simulations. We find that both methods generally have good performance with moderate and large sample sizes. MLTs slightly outperformed CPMs in small sample sizes under correct models. CPMs tended to be somewhat more robust to model misspecification and outcome rounding. Except in the simplest situations, both methods outperform basic transformation approaches commonly used in practice. We apply both methods to an HIV biomarker study.

Keywords: HIV; nonparametric maximum likelihood estimation; ordinal regression model; transformation model.

FIGURE 1

Transformation functions used in simulation and corresponding Bernstein polynomials approximation with order M

FIGURE 2

Simulation results under the primary setting

FIGURE 3

Simulation results when including covariate Z, which is dependent and independent of X

FIGURE 4

Simulation results for mixture of discrete and continuous responses comparing CPM and MLT treating response as ordinary continuous responses and censoring responses.

FIGURE 5

Simulation results for discretized continuous responses into 5, 10, 20 and 50 categories.

FIGURE 6

Results for IL-6. A: The distribution of IL-6. B: The estimated transformation functions. C: The estimated conditional means and their confidence intervals. Other covariates are at their most frequent level or median level. D: The estimated conditional medians and their confidence intervals. Other covariates are at their most frequent level or median level.

FIGURE 7

Results for hsCRP. A: The distribution of hsCRP. B: The estimated transformation functions. C: The estimated conditional means and their confidence intervals. Other covariates are at their most frequent level or median level. D: The estimated conditional medians and their confidence intervals. Other covariates are at their most frequent level or median level.

FIGURE 8

The comparison of the estimated conditional mean on the original scale and the transformed log scale

FIGURE 9

Results for IL-1-β. A: The distribution of IL-1-β. B: The estimated transformation functions. C: The estimated conditional means and their confidence intervals. Other covariates are at their most frequent level or median level. D: The estimated conditional medians and their confidence intervals. Other covariates are at their most frequent level or median level.