Heterogeneity Profoundly Alters Emergent Stress Fields in Constrained Multicellular Systems

Abstract

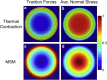
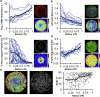
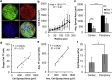
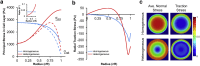
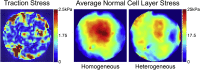
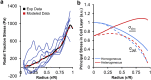
Stress fields emerging from the transfer of forces between cells within multicellular systems are increasingly being recognized as major determinants of cell fate. Current analytical and numerical models used for the calculation of stresses within cell monolayers assume homogeneous contractile and mechanical cellular properties; however, cell behavior varies by region within constrained tissues. Here, we show the impact of heterogeneous cell properties on resulting stress fields that guide cell phenotype and apoptosis. Using circular micropatterns, we measured biophysical metrics associated with cell mechanical stresses. We then computed cell-layer stress distributions using finite element contraction models and monolayer stress microscopy. In agreement with previous studies, cell spread area, alignment, and traction forces increase, whereas apoptotic activity decreases, from the center of cell layers to the edge. The distribution of these metrics clearly indicates low cell stress in central regions and high cell stress at the periphery of the patterns. However, the opposite trend is predicted by computational models when homogeneous contractile and mechanical properties are assumed. In our model, utilizing heterogeneous cell-layer contractility and elastic moduli values based on experimentally measured biophysical parameters, we calculate low cell stress in central areas and high anisotropic stresses in peripheral regions, consistent with the biometrics. These results clearly demonstrate that common assumptions of uniformity in cell contractility and stiffness break down in postconfluence confined multicellular systems. This work highlights the importance of incorporating regional variations in cell mechanical properties when estimating emergent stress fields from collective cell behavior.

Figure 1

Homogeneous thermal contraction and MSM modeling reveal high cell stress in the aggregate center and high tractions at the edge. Heat maps of traction forces for homogeneous thermal contraction (a) and MSM model (c) show high tractions along the aggregate periphery. Heat maps of cell-layer stress for homogeneous thermal contraction (b) and the MSM model (d) display high stresses in the aggregate center. To see this figure in color, go online.

Figure 2

Protein measurements for cell-layer stress indicate low stress state within the center of VIC aggregates. (a) α-SMA intensity doubles from the center to edge of the aggregate. The inset shows the aggregate stained for α-SMA (top; red) and a heat map of average (Avg.) α-SMA intensity (bottom). n = 8 images (two replicates). (b) G-/F-actin ratio with respect to the aggregate radius decreases from the center to periphery. The inset shows the aggregate (top) stained for F-actin (green), G-actin (red), and nuclei (blue) and a heat map of average G-/F-actin intensity (bottom). n = 14 images (3 replicates). (c) Cleaved caspase-3/7 presence decreases from the center to edge of the aggregate. The inset shows the aggregate stained for caspase-3/7 (top; green, dotted line indicates the aggregate edge). A heat map was generated for the average caspase-3/7 intensity (bottom). n = 24 images (1 replicate). (d) F-actin alignment index increases from the center to edge of the aggregate. An index of zero indicates no stress fiber alignment, whereas an index of one indicates perfect fiber alignment. The inset shows the aggregate stained for F-actin (top; green) and a heat map for average alignment index (bottom). n = 9 images (two replicates). (e) The left panel shows the aggregate with individual cells outlined and measured for cell angle. The center panel shows individual cell outlines. The right panel showing the angle of cell in relation to the radial angle (90° indicates perpendicular to radial angle) shows that peripheral cells circumferentially align more than central cells. n = 2 images (two replicates). Scale bars, 100 μm. To see this figure in color, go online.

Figure 3

Cells within the central region of aggregates have on average, lower spread area, lower traction force (TF), and lower indentation stiffness compared to those in the peripheral area. (a) Aggregate stained for F-actin (green), α-SMA (red), nuclei (blue), and merge is shown. Scale bars, 50 μm. (b) The measured relationship for cell area as a function of radius for one aggregate is shown. Gray dots are raw data, black dots are mean ± standard deviation for 20 μm bins, and the exponential trendline is fit to binned means. (c) The central cell spread area is approximately half that of peripheral cells. Cell spread area decreases over 1 week in culture in both central and peripheral regions. n = 22 cells for both the center and periphery at day 1, and N = 16 cells for both the center and periphery at day 7 (two replicates). Data are represented as mean ± standard deviation. ^∗∗∗ indicates p < 0.001 and ^∗∗∗∗ indicates p < 0.0001 for two-way analysis of variance with Sidak’s post hoc test. (d) The relationship for TF as a function of cell area for individual VICs is shown. (e) The relationship of average TF as a function of average area per cell in multicellular aggregates is shown. (f) Central cells in aggregates have a lower modulus from AFM indentation analysis than peripheral cells. n = 8 aggregates (three replicates). Data are represented as mean ± standard error, and ^∗ indicates p < 0.05 for Student’s t-test. To see this figure in color, go online.

Figure 4

Continuous distribution for contractile stresses as a function of radius is used to simulate cell-layer and substrate stresses. (a) Shown are cell-layer radial (dotted) and circumferential (solid) stresses with homogeneous (blue) and exponential heterogeneous (red) conditions for contractility (coefficient of thermal expansion, α, is shown graphically at the top of b). (b) Predicted radial traction stresses for homogeneous (blue) and exponential heterogeneous (red) models of cell contractility as a function of radius are shown. (c) Heat maps of predicted average normal stress and traction stresses for the homogeneous and exponential conditions are shown. To see this figure in color, go online.

Figure 5

Heat maps from left to right show measured traction stresses and output average normal stresses for homogeneous and exponential models for a representative aggregate. Distributions of cell-layer elastic moduli are homogeneous and exponentially varying modulus per equation E(r) = 0.9e^2.34r. To see this figure in color, go online.

Figure 6

Cell-layer stresses calculated by MSM for homogeneous and heterogeneous conditions from traction forces averaged over many aggregates. (a) The average radial traction stresses measured from six aggregates (blue lines) were averaged (black line) and a best fit curve (red dashed) was determined. (b) Inputting average traction stresses versus radius generates predictive models for cell-layer radial (dotted) and circumferential (solid) stresses with homogeneous (blue) and exponential heterogeneous (red) conditions for modulus. To see this figure in color, go online.