NANUQ: a method for inferring species networks from gene trees under the coalescent model

Abstract

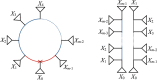
Species networks generalize the notion of species trees to allow for hybridization or other lateral gene transfer. Under the network multispecies coalescent model, individual gene trees arising from a network can have any topology, but arise with frequencies dependent on the network structure and numerical parameters. We propose a new algorithm for statistical inference of a level-1 species network under this model, from data consisting of gene tree topologies, and provide the theoretical justification for it. The algorithm is based on an analysis of quartets displayed on gene trees, combining several statistical hypothesis tests with combinatorial ideas such as a quartet-based intertaxon distance appropriate to networks, the NeighborNet algorithm for circular split systems, and the Circular Network algorithm for constructing a splits graph.

Keywords: Gene tree; Hybridization; Level-1 network; NANUQ; Network multispecies coalescent; Quartets; Species network inference.

Fig. 1

(L) A rooted phylogenetic network $N^{+}$ with root r and lowest stable ancestor m, and (R) the unrooted network $N^{-}$ induced from $N^{+}$

Fig. 2

Three quartet networks, $Q_{\mathit{abdf}}$, $Q_{\mathit{bcef}}$, and $Q_{\mathit{abcd}}$, induced from the unrooted network $N^{-}$ of Fig. 1(R)

Fig. 3

Cycles in a level-1 quartet network are classified as type $m_k$ if they have m edges and k descendants of the hybrid node. The only cycles possible in a level-1 quartet network are of (L) type $2_1$, $2_2$, and $2_3$; (C) type $3_1$ and $3_2$; and (R) type $4_1$. The dashed lines represent subgraphs that may contain other $m_k$ cycles for $m=2,3$

Fig. 4

Planar projections of the simplex ${\mathrm{\Delta }}_2$ showing types of concordance factors for networks $N_c^{-}$ of Proposition 9. (L) Gray line segments represent tree-like CFs that arise from quartet networks with no $3_2$-cycle and with no 4-cycle. (C) Gray line segments represent CFs that arise from quartet networks with a $3_2$-cycle. (R) Gray shaded areas represent CFs that arise from quartet networks containing a 4-cycle. In all three figures, the topology of $N_c^{-}$ is marked for the appropriate line segments or regions of CFs

Fig. 5

(L) NMSC parameters for an induced unrooted quartet $N^{-}$ with a $3_2$-cycle. (C) A region of tree-like parameters $(x_1,x_3)$ on $N^{-}$ for arbitrary $t_2$, $t_4$, $\gamma$. (R) A region of tree-like parameters $(x_1,M)$, where $M=max\{x_2,x_4\}$ for arbitrary $t_3$, $\gamma$. Transformed parameters are defined by $x_i=e^{-t_i}$

Fig. 6

For the tree $Q_{\mathit{abcd}}$ on the left, ${\rho }_{\mathit{ab}}(Q_{\mathit{abcd}})=0$ and ${\rho }_{\mathit{ac}}(Q_{\mathit{abcd}})=1$, since a and c are separated by ab|cd, but a and b are not. For the quartet network $Q_{\mathit{abcd}}$ on the right, ${\rho }_{\mathit{ab}}(Q_{\mathit{abcd}})=1/2$ and ${\rho }_{\mathit{ac}}(Q_{\mathit{abcd}})=1$, since the trees displayed by $Q_{\mathit{abcd}}$ are ab|cd and ad|bc

Fig. 7

(L) A cycle in a level-1 network $N^{-}$, and (R) the two simpler networks produced from it by deleting one hybrid edge. The cycle edges in these networks that arise from the original cycle are shown in blue. If $N^{-}$ has a single cycle, then the networks on the right are the two trees in $\mathcal{G}(N^{-})$

Fig. 8

An m-dart, for $m=5,6,7$ respectively. The frontier edges, shown in bold outline, are characterized in the text. The outer vertices labelled by the $X_i$ are the corners. The point of the dart is the unique corner which is $m-3$ frontier edges away from the closest corners

Fig. 9

(L) A rooted level-1 network $N^{+}$ with 2- and 3-cycles shown in light red, (C) the unrooted topological network $N^{-}$ obtained from $N^{+}$ by contracting 2- and 3-cycles and undirecting 4-cycles, and (R) a frontier-minimal splits graph that corresponds to $N^{-}$ by Theorem 34. Note that the splits graph has a 4-cycle, a 5-dart, and a 6-dart, arising from the 4-, 5-, and 6-cycles of $N^{-}$. The metric structure of the splits graph, which is not described by Theorem 34, reflects the split weights as defined by Definition 18. See also Example 37

Fig. 10

Representative simplex plots for empirical CFs, with hypothesis testing results, computed from a simulated data set of 1000 gene trees from the species network given in Table 1

Fig. 11

Simplex plots for hypothesis test results on the yeast data set, with two choices of significance levels $\alpha ={10}^{-4}$ and ${10}^{-2}$ with $\beta =0.1$. The choice of $\beta$ here is largely irrelevant, as no plotted empirical CFs are near the center. Larger $\alpha$ results in more empirical CFs being determined as supporting 4-cycles, as several blue circles on the left change to red triangles on the right

Fig. 12

Networks inferred by NANUQ for yeast data of Example 38 with $\beta =0.1$ and $\alpha ={10}^{-4}$ (L) or ${10}^{-2}$ (R)

Fig. 13

Simplex plot showing hypothesis test results for the Heliconius data set of Example 39

Fig. 14

(L) Splits graph for Heliconius data set of Example 39, for $\alpha ={10}^{-40}$, $\beta ={10}^{-30}$, and (R) NANUQ inferred network structure