The basic reproductive number for disease systems with multiple coupled heterogeneities

Abstract

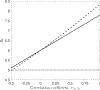
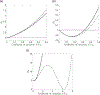
In mathematical epidemiology, a well-known formula describes the impact of heterogeneity on the basic reproductive number, R₀, for situations in which transmission is separable and for which there is one source of variation in susceptibility and one source of variation in infectiousness. This formula is written in terms of the magnitudes of the heterogeneities, as quantified by their coefficients of variation, and the correlation between them. A natural question to ask is whether analogous results apply when there are multiple sources of variation in susceptibility and/or infectiousness. In this paper we demonstrate that with three or more coupled heterogeneities, R₀ under separable transmission depends on details of the distribution of the heterogeneities in a way that is not seen in the well-known simpler situation. We provide explicit formulae for the cases of multivariate normal and multivariate log-normal distributions, showing that R₀ can again be expressed in terms of the magnitudes of the heterogeneities and the pairwise correlations between them. The formulae, however, differ between the two multivariate distributions, demonstrating that no formula of this type applies generally when there are three or more coupled heterogeneities. We see that the results of the formulae are approximately equal when heterogeneities are relatively small and show that an earlier result in the literature (Koella, 1991) should be viewed in this light. We provide numerical illustrations of our results and discuss a setting in which coupled heterogeneities are likely to have a major impact on the value of R₀. We also describe a rather surprising result: in a system with three heterogeneities, R₀ can exhibit non-monotonic behavior with increasing levels of heterogeneity, in marked contrast to the familiar two heterogeneity setting in which R₀ either increases or decreases with increasing heterogeneity.

Keywords: Basic reproductive number; Coupled heterogeneities; Disease transmission model; Heterogeneity.

Figure 1:

Comparison of R₀ values calculated for multivariate normally-distributed (solid line) and log-normally-distributed (dashed line) heterogeneities for differing values of the correlation coefficient, $r_{X_1,X_3}$, between the biting rate, X₁, and average duration of human infection, X₃. X₁ and X₃ are taken to have means equal to 1 and 5, respectively, and variances Var(X₁) = 0.2 and Var(X₃) = 4. The value of the susceptibility parameter was fixed at 1 for the entire population. Lines are obtained using the MVN and MVLN formulae (eqns 17 and 18, respectively). The horizontal dashed line denotes the value of R₀ if there was no heterogeneity, i.e. obtained using the average values, $R_0^{\mathrm{hom}}$. Note that the basic reproductive number is the same for both distributions when the correlation coefficient is equal to zero, and that this is greater than the value $R_0^{\mathrm{hom}}$ obtained using the average values because of heterogeneity in the biting rate.

Figure 2:

Comparison of R₀ values calculated for multivariate normally-distributed (solid line) and log-normally-distributed (dashed line) heterogeneities for differing values of the correlation coefficient, $r_{X_1,X_3}$, between the biting rate, X₁, and average duration of human infection, X₃. Results are presented for three different levels of the heterogeneity in the average duration of human infection: black lines have Var(X₃) = 4 (these are the lines that appear in Figure (1); blue lines have Var(X₃) = 1, while red lines have Var(X₃) = 10. As in Figure (1), X₁ and X₃ are taken to have means equal to 1 and 5, respectively, and Var(X₁) = 0.2. The value of the susceptibility parameter was fixed at 1 for the entire population. The horizontal dashed line denotes the value of R₀ if there was no heterogeneity, i.e. obtained using the average value, $R_0^{\mathrm{hom}}$.

Figure 3:

Comparison of R₀ values calculated for multivariate normally-distributed (solid line) and log-normally-distributed (dashed line) heterogeneities for differing levels of heterogeneity in the biting rate, X₁. Panel (a): positive correlation coefficient, $r_{X_1,X_3}$, between the biting rate and average duration of human infection, X₃, equal to 0.5. Panel (b): negative correlation coefficient, with $r_{X_1,X_3}=-0.4$. Panel (c): as panel (b), but with a larger range of values of CV(X₁) on the horizontal axis. Other parameter values are as in Figure 1, with X₁ and X₃ taken to have means equal to 1 and 5, respectively, and Var(X₃) = 4. The value of the susceptibility parameter was fixed at 1 for the entire population. The horizontal dashed lines denote the value of R₀ if there was no heterogeneity, i.e. obtained using the average value, $R_0^{\text{hom}}$. Note the surprising non-monotonic impact of heterogeneity in panels (b) and (c), behavior that does not occur in the well-studied case of two coupled heterogeneities.