Recovering rearranged cancer chromosomes from karyotype graphs

Abstract

Background: Many cancer genomes are extensively rearranged with highly aberrant chromosomal karyotypes. Structural and copy number variations in cancer genomes can be determined via abnormal mapping of sequenced reads to the reference genome. Recently it became possible to reconcile both of these types of large-scale variations into a karyotype graph representation of the rearranged cancer genomes. Such a representation, however, does not directly describe the linear and/or circular structure of the underlying rearranged cancer chromosomes, thus limiting possible analysis of cancer genomes somatic evolutionary process as well as functional genomic changes brought by the large-scale genome rearrangements.

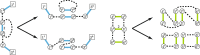
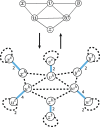
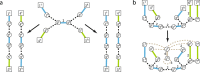
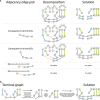
Results: Here we address the aforementioned limitation by introducing a novel methodological framework for recovering rearranged cancer chromosomes from karyotype graphs. For a cancer karyotype graph we formulate an Eulerian Decomposition Problem (EDP) of finding a collection of linear and/or circular rearranged cancer chromosomes that are determined by the graph. We derive and prove computational complexities for several variations of the EDP. We then demonstrate that Eulerian decomposition of the cancer karyotype graphs is not always unique and present the Consistent Contig Covering Problem (CCCP) of recovering unambiguous cancer contigs from the cancer karyotype graph, and describe a novel algorithm CCR capable of solving CCCP in polynomial time. We apply CCR on a prostate cancer dataset and demonstrate that it is capable of consistently recovering large cancer contigs even when underlying cancer genomes are highly rearranged.

Conclusions: CCR can recover rearranged cancer contigs from karyotype graphs thereby addressing existing limitation in inferring chromosomal structures of rearranged cancer genomes and advancing our understanding of both patient/cancer-specific as well as the overall genetic instability in cancer.

Keywords: Cancer genomics; Computational biology; Contigs; Genome rearrangements; Graph decomposition; Structural variations.

Fig. 1

Rearranged genomes and Interval Adjacency Graphs. a Reference and derived genomes R and Q both depicted as sequences of oriented segments and a weighted Interval Adjacency Graph determined by a derived genome Q. In the IAG segment edges are shown as solid, with colors corresponding to distinct chromosomes, and adjacency edges are shown as dashed, with reference adjacencies shown in black, and novel adjacencies depicted in red. Edges with copy number 0 are shown as faded, copy numbers of 1 are omitted for clarity. b Rearranged linear chromosomes in the mutated genome Q depicted as both sequences of oriented segments and as segment/adjacency edge-alternating paths in the IAG’s connected components

Fig. 2

Eulerian Decompositions of Interval Adjacency Graphs. Distinct Eulerian decompositions of different cardinalities of IAG connected components where vertices have a non-zero copy number excess (left) and with all vertices being copy number balanced (right)

Fig. 3

Reduction of K₃ covering problem to the instance of max-EDP. Transformation of the regular undirected graph G into IAG G^′ and back with K₃ decomposition in G corresponding to segment-adjacency edge-alternating cycles in G^′

Fig. 4

Eulerian decompositions and contigs covering inference for Interval Adjacency Graphs. a Two distinct contig coverings corresponding to minimal Eulerian decompositions of the same IAG. b Transformation of IAG G with vertices with copy number excess (i.e., telomere vertices) into a an IAG G^′ with no telomere vertices. Added supplemental segment and adjacency edges are shown in grey

Fig. 5

CCR workflow on IAG presented in Fig. 4b. a Iterative Step 3 in CCR workflow: processing of pairs of consecutive adjacency edges in the min-ED, contraction of pairs that are present in all min-EDs, updates of the solution. Supplemental (both segment and adjacency) edges are shown in grey, contracted adjacency edges are shown as dotted orange. b Processing of the terminal graph obtained after iterative Step 3 execution with removal of contracted adjacency edges, incident to them segment edges, and dangling edges after that. Search for a collection L of adjacency edges in which no pair {e,f} share the same copy of a segment

Fig. 6

Contigs obtained with both CCR (red) and the baseline “naive” contig inference approach (blue) and on haplotype-specific cancer karyotype graphs. a Number of contigs recovered with CCR and the “naive” approach from input karyotype graphs obtained with RCK on HATCHet CNA input. b Number of contigs recovered with CCR and the “naive” approach from input karyotype graphs obtained with RCK on Battenberg CNA input. c N50 metric for contigs recovered with CCR and “naive” approach from input karyotype graphs obtained with RCK on HATCHet CNA input. d N50 metric for contigs recovered with CCR and “naive” approach from input karyotype graphs obtained with RCK on Battenberg CNA input