Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2020 Jun 1;189(6):613-622.
doi: 10.1093/aje/kwz268.

Evaluating the Utility of Coarsened Exact Matching for Pharmacoepidemiology Using Real and Simulated Claims Data

John E Ripollone, Krista F Huybrechts, Kenneth J Rothman, Ryan E Ferguson, Jessica M Franklin

Evaluating the Utility of Coarsened Exact Matching for Pharmacoepidemiology Using Real and Simulated Claims Data

John E Ripollone et al. Am J Epidemiol. .

Abstract

Coarsened exact matching (CEM) is a matching method proposed as an alternative to other techniques commonly used to control confounding. We compared CEM with 3 techniques that have been used in pharmacoepidemiology: propensity score matching, Mahalanobis distance matching, and fine stratification by propensity score (FS). We evaluated confounding control and effect-estimate precision using insurance claims data from the Pharmaceutical Assistance Contract for the Elderly (1999-2002) and Medicaid Analytic eXtract (2000-2007) databases (United States) and from simulated claims-based cohorts. CEM generally achieved the best covariate balance. However, it often led to high bias and low precision of the risk ratio due to extreme losses in study size and numbers of outcomes (i.e., sparse data bias)-especially with larger covariate sets. FS usually was optimal with respect to bias and precision and always created good covariate balance. Propensity score matching usually performed almost as well as FS, especially with higher index exposure prevalence. The performance of Mahalanobis distance matching was relatively poor. These findings suggest that CEM, although it achieves good covariate balance, might not be optimal for large claims-database studies with rich covariate information; it might be ideal if only a few (<10) strong confounders must be controlled.

Keywords: Mahalanobis distance matching; coarsened exact matching; covariate balance; fine stratification; plasmode simulation; propensity score; propensity score matching.

PubMed Disclaimer

Figures

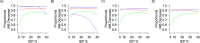
Figure 1
Figure 1
Results of plasmode analysis, noninteraction scenarios—average proportional decrease in Mahalanobis balance. A) Very small covariate set scenarios. B) Small covariate set scenarios. C) Standard covariate set scenarios. D) Large covariate set scenarios. Blue: coarsened exact matching trends; green: propensity score matching trends; purple: Mahalanobis distance matching trends; and red: fine-stratification-by-propensity-score trends. IEP, index exposure prevalence; MB, Mahalanobis balance.
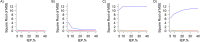
Figure 2
Figure 2
Results of plasmode analysis, noninteraction scenarios—square root of mean squared error (MSE), including coarsened exact matching results. A) Very small covariate set scenarios. B) Small covariate set scenarios. C) Standard covariate set scenarios. D) Large covariate set scenarios. Blue: coarsened exact matching trends; green: propensity score matching trends; purple: Mahalanobis distance matching trends; and red: fine-stratification-by-propensity-score trends. IEP, index exposure prevalence.
Figure 3
Figure 3
Results of plasmode analysis, noninteraction scenarios—square root of mean squared error (MSE), excluding coarsened exact matching results. A) Very small covariate set scenarios. B) Small covariate set scenarios. C) Standard covariate set scenarios. D) Large covariate set scenarios. Green: propensity score matching trends; purple: Mahalanobis distance matching trends; and red: fine-stratification-by-propensity-score trends. IEP, index exposure prevalence.
See this image and copyright information in PMC

References

    1. Iacus SM, King G, Porro G. Causal inference without balance checking: coarsened exact matching. Political Analysis. 2011;20(1):1–24.
    1. Iacus SM, King G, Porro G. Multivariate matching methods that are monotonic imbalance bounding. J Am Stat Assoc. 2011;106(493):345–361.
    1. King G, Nielsen R. Why propensity scores should not be used for matching. Political Analysis. 2019;27(4):435–454.
    1. King G, Nielsen R, Coberley C, et al. Comparative effectiveness of matching methods for causal inference.http://gking.harvard.edu/publications/comparative-effectiveness-matching.... Accessed December 1, 2018.
    1. Ripollone JE, Huybrechts KF, Rothman KJ, et al. . Implications of the propensity score matching paradox in pharmacoepidemiology. Am J Epidemiol. 2018;187(9):1951–1961. - PMC - PubMed

Publication types