Phase-Dependent Response to Afferent Stimulation During Fictive Locomotion: A Computational Modeling Study

Abstract

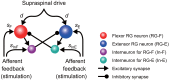
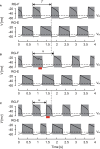
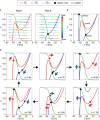
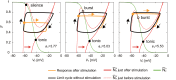
Central pattern generators (CPGs) in the spinal cord generate rhythmic neural activity and control locomotion in vertebrates. These CPGs operate under the control of sensory feedback that affects the generated locomotor pattern and adapt it to the animal's biomechanics and environment. Studies of the effects of afferent stimulation on fictive locomotion in immobilized cats have shown that brief stimulation of peripheral nerves can reset the ongoing locomotor rhythm. Depending on the phase of stimulation and the stimulated nerve, the applied stimulation can either shorten or prolong the current locomotor phase and the locomotor cycle. Here, we used a mathematical model of a half-center CPG to investigate the phase-dependent effects of brief stimulation applied to CPG on the CPG-generated locomotor oscillations. The CPG in the model consisted of two half-centers mutually inhibiting each other. The rhythmic activity in each half-center was based on a slowly inactivating, persistent sodium current. Brief stimulation was applied to CPG half-centers in different phases of the locomotor cycle to produce phase-dependent changes in CPG activity. The model reproduced several results from experiments on the effect of afferent stimulation of fictive locomotion in cats. The mechanisms of locomotor rhythm resetting under different conditions were analyzed using dynamic systems theory methods.

Keywords: afferent control of CPG; central pattern generator; dynamic structure; half-center CPG; phase-dependent response.

Figure 1

Model schematic of the rhythm generator (RG) network and afferent inputs. The RG network is composed of flexor (RG-F) and extensor (RG-E) centers inhibiting each other via inhibitory interneurons In-F and In-E, respectively. The supraspinal drive provides excitation to the RG-F and RG-E neurons defining the frequency of oscillations. Sensory afferents can synaptically excite both RG neurons and inhibitory interneurons.

Figure 2

Changes of membrane potential of RG-F (top panel) and RG-E (bottom panel) neurons (A) without any stimulation, (B) with stimulation applied to the flexor side during flexor phase, and (C) with stimulation applied to the flexor side during extensor phase. The red bars indicate the application of stimulation. Gray regions indicate active phases. The applied stimulation increased the duration of the current flexor phase and cycle period in (B) and initiated the flexor phase and decreased the cycle period in (C). Both stimulations produced phase shifts.

Figure 3

(A) Phase-dependent response of the RG-F neuron by stimulating sensory fibers of the flexor side. (B) Response against flexor muscle stimulation during fictive locomotion in cats (adapted from Schomburg et al., 1998). The flexion (extension) phase corresponds to the active (silent) phase of the RG-F neuron of the CPG model. (C) Phase-dependent response of the RG-F neuron by stimulating sensory inputs on the extensor side.

Figure 4

Roles of nullclines of RG-F and RG-E neurons to produce oscillatory behaviors. The green lines show ${\widehat{\text{N}}}_{\text{F}}^{\text{h}}$ and ${\widehat{\text{N}}}_{\text{E}}^{\text{h}}$. The red and blue lines show ${\widehat{\text{N}}}_{\text{F}}^{\text{V}}$ and ${\widehat{\text{N}}}_{\text{E}}^{\text{V}}$, respectively. Circles indicate intersections of nullclines [filled circles for both negative eigenvalues (stable node) and open circles for negative and positive eigenvalues (saddle)]. (A) ${\widehat{\text{N}}}_{\text{F}}^{\text{V}}$ and ${\widehat{\text{N}}}_{\text{E}}^{\text{V}}$ with the vector field for the case without synaptic connections from other neurons. The saddle produces a limit cycle (orange orbit) while stable node does not produce any oscillatory behavior. (B) Schematic illustration of changes in ${\widehat{\text{N}}}_{\text{F}}^{\text{V}}$ and ${\widehat{\text{N}}}_{\text{E}}^{\text{V}}$ induced by synaptic connections from other neurons. The intersection of ${\widehat{\text{N}}}_{\text{F}}^{\text{V}}$ and ${\widehat{\text{N}}}_{\text{F}}^{\text{h}}$ almost remains saddle (burst mode), which induces an oscillatory behavior. On the other hand, ${\widehat{\text{N}}}_{\text{E}}^{\text{V}}$ transitions between two positions depending on the inhibitory signal from the contralateral side. This transition produces oscillatory behavior between tonic and silence modes for the extensor side. (C) Detailed illustration of our model at ϕ = 0, 0.89, 1.78, 2.68, 3.88, and 5.08 rad. Red and blue diamonds are (V_F, h_F) and (V_E, h_E), respectively, and these points move in accordance with eigenvalues, as indicated by arrows.

Figure 5

Response of a RG-F neuron on the V_F-h_F plane by stimulating the flexor side at ϕ_s = 3.77, 5.03, and 5.53 rad. The black line shows the limit cycle without stimulation. Stimulation is applied at filled orange circles. Disturbed trajectories (orange line) take a shortcut to enter the limit cycle at different positions depending on ϕ_s. Earlier ϕ_s has a larger truncated trajectory. The green line shows ${\widehat{\text{N}}}_{\text{F}}^{\text{h}}$. The red dashed and solid lines show ${\widehat{\text{N}}}_{\text{F}}^{\text{V}}$ just before and after the stimulation, respectively. The intersection of ${\widehat{\text{N}}}_{\text{F}}^{\text{h}}$ and ${\widehat{\text{N}}}_{\text{F}}^{\text{V}}$ changed from silence or burst mode to tonic mode by the stimulation.

Figure 6

(A) Response of RG-E neuron on the V_E-h_E plane by stimulating the extensor side at ϕ_s = 1.13 rad. The black line shows the limit cycle without stimulation. Stimulation was applied at filled cyan circle. The blue dashed and solid lines show ${\widehat{\text{N}}}_{\text{E}}^{\text{V}}$ just before and after the stimulation, respectively. While ${\widehat{\text{N}}}_{\text{E}}^{\text{V}}$ moved to the right just after the stimulation and the intersection with ${\widehat{\text{N}}}_{\text{E}}^{\text{h}}$ (green line) became tonic mode, the disturbed trajectory (cyan line) moved to the right without entering the limit cycle (①). ${\widehat{\text{N}}}_{\text{E}}^{\text{V}}$ gradually further moved to the right (blue double line shows ${\widehat{\text{N}}}_{\text{E}}^{\text{V}}$ at 80 ms after the stimulation) and the trajectory was finally cut short to the limit cycle (②). (B) Time profiles of four neurons from the onset of the stimulation to the end of the shortcut. The vertical lines show the onset and 80 ms after the stimulation. The horizontal line shows V_th. After the stimulation, the membrane potentials of the RG-E and In-E neurons rapidly changed and crossed over V_th (①). After that, while the membrane potentials of the RG-F and In-F neurons decreased due to the inhibitory signal from the In-E neuron and crossed over V_th, the membrane potential of the RG-E neuron gradually increased. As a result, the decrease of the inhibitory signal from the flexor side increased the activity of the RG-E, which induced the shortcut (②).

Figure 7

Change of ${\widehat{\text{N}}}_{\text{F}}^{\text{V}}$ and ${\widehat{\text{N}}}_{\text{E}}^{\text{V}}$ by stimulation at the end of the active phase of (A) the flexor side (ϕ_s = 2.39 rad) and (B) the extensor side (ϕ_s = 5.91 rad). Solid and dotted lines show the results of the cases with and without the stimulation, respectively. Red and blue diamonds mark the positions of (V_F, h_F) and (V_E, h_E), respectively (filled diamonds for stimulation and open diamonds for non-stimulation). In (A), the stimulation moved ${\widehat{\text{N}}}_{\text{F}}^{\text{V}}$ to the right and changed the intersection of ${\widehat{\text{N}}}_{\text{F}}^{\text{h}}$ and ${\widehat{\text{N}}}_{\text{F}}^{\text{V}}$ from burst to tonic mode. Furthermore, ${\widehat{\text{N}}}_{\text{F}}^{\text{V}}$ showed almost no change for a while. These prolonged the activity duration. In addition, they kept the intersection of ${\widehat{\text{N}}}_{\text{E}}^{\text{V}}$ and ${\widehat{\text{N}}}_{\text{E}}^{\text{h}}$ silence mode for a while, which also delayed the neural activity. In (B), the stimulation moved ${\widehat{\text{N}}}_{\text{E}}^{\text{V}}$ to the right and maintained the intersection of ${\widehat{\text{N}}}_{\text{F}}^{\text{h}}$ and ${\widehat{\text{N}}}_{\text{F}}^{\text{V}}$ in tonic mode. These prolonged the activity duration of the RG-E neuron.