Effect of Teaching Bayesian Methods Using Learning by Concept vs Learning by Example on Medical Students' Ability to Estimate Probability of a Diagnosis: A Randomized Clinical Trial

Abstract

Importance: Clinicians use probability estimates to make a diagnosis. Teaching students to make more accurate probability estimates could improve the diagnostic process and, ultimately, the quality of medical care.

Objective: To test whether novice clinicians can be taught to make more accurate bayesian revisions of diagnostic probabilities using teaching methods that apply either explicit conceptual instruction or repeated examples.

Design, setting, and participants: A randomized clinical trial of 2 methods for teaching bayesian updating and diagnostic reasoning was performed. A web-based platform was used for consent, randomization, intervention, and testing of the effect of the intervention. Participants included 61 medical students at McMaster University and Eastern Virginia Medical School recruited from May 1 to September 30, 2018.

Interventions: Students were randomized to (1) receive explicit conceptual instruction regarding diagnostic testing and bayesian revision (concept group), (2) exposure to repeated examples of cases with feedback regarding posttest probability (experience group), or (3) a control condition with no conceptual instruction or repeated examples.

Main outcomes and measures: Students in all 3 groups were tested on their ability to update the probability of a diagnosis based on either negative or positive test results. Their probability revisions were compared with posttest probability revisions that were calculated using the Bayes rule and known test sensitivity and specificity.

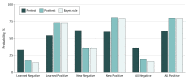
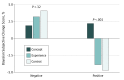
Results: Of the 61 participants, 22 were assigned to the concept group, 20 to the experience group, and 19 to the control group. Approximate age was 25 years. Two participants were first-year; 37, second-year; 12, third-year; and 10, fourth-year students. Mean (SE) probability estimates of students in the concept group were statistically significantly closer to calculated bayesian probability than the other 2 groups (concept, 0.4%; [0.7%]; experience, 3.5% [0.7%]; control, 4.3% [0.7%]; P < .001). Although statistically significant, the differences between groups were relatively modest, and students in all groups performed better than expected, based on prior reports in the literature.

Conclusions and relevance: The study showed a modest advantage for students who received theoretical instruction on bayesian concepts. All participants' probability estimates were, on average, close to the bayesian calculation. These findings have implications for how to teach diagnostic reasoning to novice clinicians.

Trial registration: ClinicalTrials.gov identifier: NCT04130607.

Figure 1.. Participant Flow Diagram

The process of randomization, study completion, and analysis for students allocated to the 3 conditions.

Figure 2.. Participants’ Estimates of Pretest Probability, Posttest Probability, and the Calculated Probability Based on Bayes Rule

Cases with negative test results and positive test results by whether the cases were learned cases or new cases, and all cases.

Figure 3.. Difference Between the Calculated Bayesian Change Score and the Subjective Change Score for Each Intervention Group by Positive or Negative Test Results