Time-dependent diffusion in undulating thin fibers: Impact on axon diameter estimation
- PMID: 31868995
- PMCID: PMC7027526
- DOI: 10.1002/nbm.4187
Time-dependent diffusion in undulating thin fibers: Impact on axon diameter estimation
Abstract
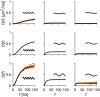
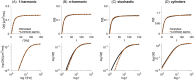
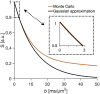
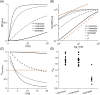
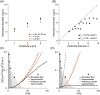
Diffusion MRI may enable non-invasive mapping of axonal microstructure. Most approaches infer axon diameters from effects of time-dependent diffusion on the diffusion-weighted MR signal by modeling axons as straight cylinders. Axons do not, however, propagate in straight trajectories, and so far the impact of the axonal trajectory on diameter estimation has been insufficiently investigated. Here, we employ a toy model of axons, which we refer to as the undulating thin fiber model, to analyze the impact of undulating trajectories on the time dependence of diffusion. We study time-dependent diffusion in the frequency domain and characterize the diffusion spectrum by its height, width, and low-frequency behavior (power law exponent). Results show that microscopic orientation dispersion of the thin fibers is the main parameter that determines the characteristics of the diffusion spectra. At lower frequencies (longer diffusion times), straight cylinders and undulating thin fibers can have virtually identical spectra. If the straight-cylinder assumption is used to interpret data from undulating thin axons, the diameter is overestimated by an amount proportional to the undulation amplitude and microscopic orientation dispersion of the fibers. At higher frequencies (shorter diffusion times), spectra from cylinders and undulating thin fibers differ. The low-frequency behavior of the spectra from the undulating thin fibers may also differ from that of cylinders, because the power law exponent of undulating fibers can reach values below 2 for experimentally relevant frequency ranges. In conclusion, we argue that the non-straight nature of axonal trajectories should not be overlooked when analyzing and interpreting diffusion MRI data.
Keywords: axon diameter; axonal trajectories; diffusion MRI; diffusion spectrum; low frequency; restricted diffusion; time dependence; undulation.
© 2019 The Authors. NMR in Biomedicine published by John Wiley & Sons Ltd.
Figures


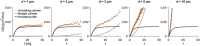

References
-
- Aboitiz F, Scheibel AB, Fisher RS, Zaidel E. Fiber composition of the human corpus callosum. Brain Res. 1992;598(1):143‐153. - PubMed
-
- Ritchie JM. On the relation between fibre diameter and conduction velocity in myelinated nerve fibres. Proc R Soc Lond B. 1982;217(1206):29‐35. - PubMed
-
- Alexander DC, Dyrby TB, Nilsson M, Zhang H. Imaging brain microstructure with diffusion MRI: practicality and applications. NMR Biomed. 2017;32(4):e3841. - PubMed
-
- Stanisz GJ, Wright GA, Henkelman RM, Szafer A. An analytical model of restricted diffusion in bovine optic nerve. Magn Reson Med. 1997;37(1):103‐111. - PubMed
-
- Assaf Y, Mayk A, Cohen Y. Displacement imaging of spinal cord using q‐space diffusion‐weighted MRI. Magn Reson Med. 2000;44(5):713‐722. - PubMed
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources

