Tractography in the presence of multiple sclerosis lesions

Abstract

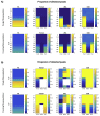
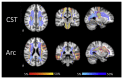
Accurate anatomical localisation of specific white matter tracts and the quantification of their tract-specific microstructural damage in conditions such as multiple sclerosis (MS) can contribute to a better understanding of symptomatology, disease evolution and intervention effects. Diffusion MRI-based tractography is being used increasingly to segment white matter tracts as regions-of-interest for subsequent quantitative analysis. Since MS lesions can interrupt the tractography algorithm's tract reconstruction, clinical studies frequently resort to atlas-based approaches, which are convenient but ignorant to individual variability in tract size and shape. Here, we revisit the problem of individual tractography in MS, comparing tractography algorithms using: (i) The diffusion tensor framework; (ii) constrained spherical deconvolution (CSD); and (iii) damped Richardson-Lucy (dRL) deconvolution. Firstly, using simulated and in vivo data from 29 MS patients and 19 healthy controls, we show that the three tracking algorithms respond differentially to MS pathology. While the tensor-based approach is unable to deal with crossing fibres, CSD produces spurious streamlines, in particular in tissue with high fibre loss and low diffusion anisotropy. With dRL, streamlines are increasingly interrupted in pathological tissue. Secondly, we demonstrate that despite the effects of lesions on the fibre orientation reconstruction algorithms, fibre tracking algorithms are still able to segment tracts that pass through areas with a high prevalence of lesions. Combining dRL-based tractography with an automated tract segmentation tool on data from 131 MS patients, the cortico-spinal tracts and arcuate fasciculi could be reconstructed in more than 90% of individuals. Comparing tract-specific microstructural parameters (fractional anisotropy, radial diffusivity and magnetisation transfer ratio) in individually segmented tracts to those from a tract probability map, we show that there is no systematic disease-related bias in the individually reconstructed tracts, suggesting that lesions and otherwise damaged parts are not systematically omitted during tractography. Thirdly, we demonstrate modest anatomical correspondence between the individual and tract probability-based approach, with a spatial overlap between 35 and 55%. Correlations between tract-averaged microstructural parameters in individually segmented tracts and the probability-map approach ranged between r=.53 (p<.001) for radial diffusivity in the right cortico-spinal tract and r=.97 (p<.001) for magnetisation transfer ratio in the arcuate fasciculi. Our results show that MS white matter lesions impact fibre orientation reconstructions but this does not appear to hinder the ability to anatomically reconstruct white matter tracts in MS. Individual tract segmentation in MS is feasible on a large scale and could prove a powerful tool for investigating diagnostic and prognostic markers.

Keywords: Brain MRI; Diffusion tensor imaging; Multiple sclerosis lesions; Spherical harmonic deconvolution; Tractography.

Fig. 1. Comparison of the three fibre orientation reconstruction algorithms in simulated data.

Simulated substrates varied in their intracellular volume fraction (ICFV). The parallel cylinders in each substrate were aligned with the z-axis (single fibre population), or with the z- as well as the y-axis (crossing fibre populations). A: For each approach (tensor-based, dRL and CSD), we calculated the percentage of all voxels within each substrate type for which the ‘true’ underlying fibre configuration peak(s) could be detected. As a control, we also calculated this percentage for ‘false’ peaks (orthogonal to the true peak(s)). In each case, the left-most plot shows the FA for each substrate type. B: Dispersion across all detected peaks of a substrate type was calculated. Dispersion was high across wrongly detected peaks, while for substrates with higher intracellular volume fraction, the true detected peaks by dRL and CSD consistently showed dispersion of < .15.

Fig. 2. Example for fibre orientation reconstruction in a patient with severe white matter damage.

Left: an axial slice of the T1-weighted scan of an MS patient is shown, highlighting an area around the posterior corona radiata that is affected by T1-hypointense lesional pathology. Right: Voxel-wise tensor (top) and FODs (middle: CSD; bottom: dRL) are shown in this area, which includes normal appearing white matter, a T1-hypointense white matter lesion and CSF in the lateral ventricle. The increased isotropic diffusion that is found in the most hypointense voxels of the lesion is reflected by tensor and FOD shapes that are comparable to the shapes found in CSF. The less hypointense voxels of the lesion show FOD shapes comparable to normal appearing white matter, but decreased in peak amplitude.

Fig. 3. Tract probability.

Tract probability maps for patients (red-yellow) are overlaid with lesion probability maps (blue-lightblue). Data from 123 to 130 patients contributed to the map for the left and right CST, respectively, and data from 130 to 122 patients contributed to the map for the left and right Arc, respectively. The lesion probability map is the same as reported in Lipp et al. (2019). Both maps are thresholded between 5 and 50%. Maps for the CST (top) and Arc (bottom) show that areas of high lesion probability overlap with the tracts. This suggests that the investigated tracts go through areas with increased likelihood of lesions, potentially affecting the tracking. R indicates the right hemisphere. Acronyms: CST: cortico-spinal tract, Arc: arcuate fasciculus.

Fig. 4. Anatomical overlap.

An overlap score between the tract probability map and the individual tract mask (registered to MNI space) were calculated. Each time, boxplots for patients (red) and controls (blue) are presented for each tract. Mean ± SD of the weighted Dice coefficients (converted to %) are 45±14 (MS) and 55±13 (HC) for the left CST, 57±8 (MS) and 60±6 (HC) for the right CST, 45±8 (MS) and 36±8 (HC) for the left Arc, and 32±9 (MS) and 35±8 (HC) for the right Arc. Data from 123 to 130 patients and 19 controls contributed to the plot for the left and right CST, respectively, and data from 130 to 122 patients and 19 controls contributed to the map for the left and right Arc, respectively. Acronyms: l: left, r: right, CST: cortico-spinal tract, Arc: arcuate fasciculus.

Fig. 5. Correlations between tract-specific microstructure from individually segmented and probability-based tracts.

For each microstructural metric (top row: FA, middle row: RD and bottom row: MTR) and tract (CST: left column, ARC: right column), the correlation between individual approach and probability-based approach is shown. Data were collapsed across hemispheres for plotting. Pearson correlation coefficients are provided for each group and hemisphere separately. MS data points are plotted in red, HC data points in blue. Data from 123 to 130 patients and 19 controls contributed to the plot for the left and right CST, respectively, and data from 130 to 122 patients and 19 controls contributed to the plot for the left and right Arc, respectively. **p < .0001. Acronyms: CST: cortico-spinal tract, Arc: arcuate fasciculus.