Improvement of the memory function of a mutual repression network in a stochastic environment by negative autoregulation

Abstract

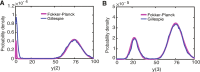
Background: Cellular memory is a ubiquitous function of biological systems. By generating a sustained response to a transient inductive stimulus, often due to bistability, memory is central to the robust control of many important biological processes. However, our understanding of the origins of cellular memory remains incomplete. Stochastic fluctuations that are inherent to most biological systems have been shown to hamper memory function. Yet, how stochasticity changes the behavior of genetic circuits is generally not clear from a deterministic analysis of the network alone. Here, we apply deterministic rate equations, stochastic simulations, and theoretical analyses of Fokker-Planck equations to investigate how intrinsic noise affects the memory function in a mutual repression network.

Results: We find that the addition of negative autoregulation improves the persistence of memory in a small gene regulatory network by reducing stochastic fluctuations. Our theoretical analyses reveal that this improved memory function stems from an increased stability of the steady states of the system. Moreover, we show how the tuning of critical network parameters can further enhance memory.

Conclusions: Our work illuminates the power of stochastic and theoretical approaches to understanding biological circuits, and the importance of considering stochasticity when designing synthetic circuits with memory function.

Keywords: Bistability; Fokker-Planck; Hill coefficient; Memory; Mutual repression; Negative autoregulation; Probability density; Stochasticity.

Fig. 1

Schematic of the mutual repression network model with negative autoregulation. Wiring diagram of the mutual repression network with negative autoregulation (MRN-NA) model. The added negative autoregulation reactions that regulate the protein synthesis of y(2) and y(3) are highlighted in red. All reaction rate constants k and dissociation constants K are listed in Tables 1 and 2. In this work, the MRN-NA is compared to the previously published MRN [12] that is identical with the exception of the negative autoregulation loops. In addition, a simplified wiring diagram is shown

Fig. 2

Deterministic and stochastic simulations of the MRN-NA model. a Deterministic simulation of the time evolution of the concentrations proteins y(1), y(2) and y(3) for different Hill coefficients. The input signal S is applied from simulation steps 250 to 500. The dissociation constants are set to K(2) = K(4) = 43; all other corresponding parameter values are set as the same as the previously published MRN [12] (Table 2). The simulated time evolution is shown for y(2) and y(3) at n = 7 (red and magenta lines), and at n = 8 (black and cyan lines). b The hysteresis curves of y(2) at different Hill coefficients n = 7 and n = 8 are consistent with the numerical integration of the rate equations. c The hysteresis curves of y(3) at different Hill coefficients n = 7 and n = 8 are consistent with the numerical integration of the rate equations. d Trajectories of the stochastic simulation of y(1), y(2) and y(3) at Hill coefficient n = 7. e Trajectories of the stochastic simulation of y(1), y(2) and y(3) at Hill coefficient n = 8. f, g Stochastic fluctuations in the MRN and MRN-NA models during the interval from simulation step 270 to 500, and F during the period from simulation steps 500 to 750. g The coefficients of variation (CVs) from the simulated stochastic trajectories during the signal period as a function of changing dissociation constants K(2) = K(4)at Hill coefficient n = 8. For more optimal comparability between the two models, the parameters associated to the negative autoregulation reactions were tuned to conserve the high steady state levels between both models. Shown are the CVs of y(2) (MRN: red line; MRN-NA: black line), and y(3) (MRN: magenta line; MRN-NA: cyan line)

Fig. 3

Phase diagram of the memory regions for the MRN and the MRN-NA models. Comparison of the memory regions of the MRN and MRN-NA models. The deterministic (solid line) and stochastic (dotted line) memory regions of the MRN are shown together with the deterministic (green area) and stochastic (red area) memory regions of the MRN-NA as function of the Hill coefficient and dissociation constants

Fig. 4

Phase diagram of the stochastic bistable regions. Phase diagrams of the stochastic bistable regions as a function of Hill coefficient and dissociation constant in the mutual repression cycle, a for y(2) in the MRN (dotted line area) and MRN-NA (red area), and b for y(3) in the MRN (dotted line area) and MRN-NA (cyan area) models

Fig. 5

Mean first passage time (MFPT) analysis. a The logarithmic MFPTs of the lower and upper steady states of y(2) (T_L and T_U) and y(3) (T_L and T_U) are shown for the MRN and MRN-NA models as a function of the Hill coefficient n at dissociation constants K(2) = K(4) = 15. b The logarithmic MFPTs of the lower and upper steady states of y(2) and y(3) denoted as above are shown for the MRN and MRN-NA as a function of the dissociation constant K(2) = K(4) at the Hill coefficient n = 3. c The logarithmic MFPTs of the lower and upper steady states of y(2) and y(3) denoted as above are shown for the MRN-NA as a function of the negative autoregulation constants k(9) = k(10) at the dissociation constants K(2) = K(4) = 15 and Hill coefficient n = 3

Fig. 6

Probability density of the steady-state levels. a Probability density of y(2) in the MRN and the MRN-NA as a function of the Hill coefficient, and b probability density of y(3) in the MRN and the MRN-NA as a function of the Hill coefficient at the dissociation constant K(2) = K(4) = 12. c Probability density of y(2) in the MRN and the MRN-NA as a function of the dissociation constant. d Probability density of y(3) in the MRN and the MRN-NA as a function of the dissociation constant at the Hill coefficient n = 3

Fig. 7

Probability density profile of the MRN-NA model. Probability densities are computed from the Fokker-Planck equations of the MRN-NA model. a Probability density of y(2), and b probability density of y(3). The parameters are given as S = 0, k(1) = 100, k(2) = 1, K(1) = K(3) = 9, K(2) = K(4) = 43, K(5) = K(6) = 9, k(3) = k(6) = 18.1, k(9) = k(10) = 4.1, k(4) = 61.04> k(7) = 43.1, k(5) = k(8) = 0.8, n = 8 for the MRN-NA model

Fig. 8

Probability density profile of the MRN and MRN-NA models in log space. Probability densities are computed from the Fokker-Planck equations of the MRN and MRN-NA models. a, b Probability density of y(2) in A the MRN and b the MRN-NA models. c, d Probability density of y(3) in C the MRN and d the MRN-NA models. The parameters for the MNA model are S = 0, k(1) = 100,k(2) = 1,K(1) = K(3) = 9, K(2) = K(4) = 43, k(3) = k(6) = 18.1, k(4) = 61.23> k(7) = 43.1, k(5) = k(8) = 0.8, n = 8. The parameters for the MRN-NA model are S = 0,k(1) = 100,k(2) = 1,K(1) = K(3) = 9,K(2) = K(4) = 43,K(5) = K(6) = 9, k(3) = k(6) = 18.1, k(9) = k(10) = 4.1, k(4) = 61.04> k(7) = 43.1, k(5) = k(8) = 0.8, n = 8. For stochastic simulations, three independent trajectories are shown