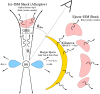
Kilonovae

Abstract

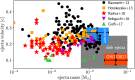
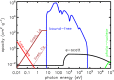
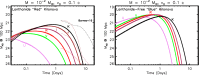
The coalescence of double neutron star (NS-NS) and black hole (BH)-NS binaries are prime sources of gravitational waves (GW) for Advanced LIGO/Virgo and future ground-based detectors. Neutron-rich matter released from such events undergoes rapid neutron capture (r-process) nucleosynthesis as it decompresses into space, enriching our universe with rare heavy elements like gold and platinum. Radioactive decay of these unstable nuclei powers a rapidly evolving, approximately isotropic thermal transient known as a "kilonova", which probes the physical conditions during the merger and its aftermath. Here I review the history and physics of kilonovae, leading to the current paradigm of day-timescale emission at optical wavelengths from lanthanide-free components of the ejecta, followed by week-long emission with a spectral peak in the near-infrared (NIR). These theoretical predictions, as compiled in the original version of this review, were largely confirmed by the transient optical/NIR counterpart discovered to the first NS-NS merger, GW170817, discovered by LIGO/Virgo. Using a simple light curve model to illustrate the essential physical processes and their application to GW170817, I then introduce important variations about the standard picture which may be observable in future mergers. These include $\sim$ hour-long UV precursor emission, powered by the decay of free neutrons in the outermost ejecta layers or shock-heating of the ejecta by a delayed ultra-relativistic outflow; and enhancement of the luminosity from a long-lived central engine, such as an accreting BH or millisecond magnetar. Joint GW and kilonova observations of GW170817 and future events provide a new avenue to constrain the astrophysical origin of the r-process elements and the equation of state of dense nuclear matter.

Keywords: Black holes; Gravitational waves; Neutron stars; Nucleosynthesis; Radiative transfer.

Fig. 1

Summary of the electromagnetic counterparts of NS–NS and BH–NS mergers and their dependence on the viewing angle with respect to the axis of the GRB jet. The kilonova, in contrast to the GRB and its afterglow, is relatively isotropic and thus represents the most promising counterpart for the majority of GW-detected mergers Image reproduced with permission from Metzger and Berger (2012), copyright by AAS

Fig. 2

Schematic timeline of the development kilonova models in the space of peak luminosity and peak timescale. The wavelength of the predicted spectral peak are indicated by color as marked in the figure. Shown for comparison are the approximate properties of the “red” and “blue” kilonova emission components observed following GW170817 (e.g., Cowperthwaite et al. ; Villar et al. 2017)

Fig. 3

Luminosity versus time after the merger of a range of heating sources relevant to powering kilonovae. Left: sources of radioactive heating include the decay of $\sim {10}^{-2}{M}_{\odot }$ of r-process nuclei, as first modeled in a parametrized way by Li and Paczyński (1998) (Eq. 4, grey band) and then by Metzger et al. (2010b) using a full reaction network, plotted here using the analytic fit of Korobkin et al. (2012) (Eq. 22, black line) and including the thermalization efficiency of Barnes et al. (2016) (Eq. 25). The outermost layers of the ejecta may contain $\sim {10}^{-4}{M}_{\odot }$ free neutrons (red line), which due to their comparatively long half-life can enhance the kilonova emission during the first few hours if present in the outermost layers of the ejecta due to premature freeze-out of the r-process (Sect. 6.1.1). Right: heating sources from a central engine. These include fall-back accretion (blue lines), shown separately for NS–NS (solid line) and BH–NS (dashed line) mergers, based on results by Rosswog (2007) for an assumed jet efficiency ${ϵ}_j=0.1$ (Eq. 34). Also shown is the rotational energy input from the magnetic dipole spin-down of a stable magnetar remnant with an initial spin period of $P=0.7$ ms and dipole field strengths of $B={10}^{15}$ G (brown lines) and ${10}^{16}$ G (orange lines). Dashed lines show the total spin-down luminosity $L_{\mathrm{sd}}$ (Eq. 36), while solid lines show the effective luminosity available to power optical/X-ray emission once accounting for suppression of the efficiency of thermalization due to the high scattering opacity of $e^{\pm }$ pairs in the nebula (Eq. 39; Metzger and Piro, 2014). The isotropic luminosity of the temporally-extended X-ray emission observed following the short GRB 080503 is shown with a green line (for an assumed source redshift $z=0.3$; Perley et al. 2009)

Fig. 4

Left: properties of the merger ejecta which affect the EM emission as a function of the binary chirp mass ${\mathcal{M}}_{\mathrm{c}}$ (Eq. 1), taken here as a proxy for the total binary mass $M_{\mathrm{tot}}$. Vertical dashed lines delineate the threshold masses for different merger remnants as marked, for an example EOS with $M_{\mathrm{TOV}}=2.1M_{\odot }$ and radius $R_{1.6}=12$ km of a $1.6M_{\odot }$ NS. The top panel shows the ejecta kinetic energy, which we take to be the sum of the initial kinetic energy of the ejecta (estimated using fits to numerical relativity simulations; Coughlin et al. 2018, 2019) and, in the case of stable or SMNSs, the rotational energy which can be extracted from the remnant before forming a BH (Margalit and Metzger 2017). The bottom panel shows the ejecta mass, both dynamical and disk wind ejecta, estimated as in Coughlin et al. (2019), where 50% of the disk mass is assumed to be ejected at $v=0.15$ c (e.g., Siegel and Metzger 2017). The finite width of the lines results from a range of binary mass ratio $q=0.7$–1, to which the tidal dynamical ejecta is most sensitive. The ejecta mass line is colored qualitatively according to the dominant color of the kilonova emission, which becomes redder for more massive binaries (with shorter-lived remnants) due to their more neutron-rich ejecta (Metzger and Fernández 2014). Right: distribution of BNS merger chirp masses drawn from a NS population representative of Galactic double NSs (Kiziltan et al. 2013). Dashed vertical curves separate the ${\mathcal{M}}_{\mathrm{c}}$ parameter space based on the possible merger outcomes in each region. The fraction of mergers expected to occur in each region (the integral over the PDF within this region) is stated above the region in red (see also Table 3) Image reproduced with permission from Margalit and Metzger (2019), copyright by the authors

Fig. 5

Dynamical ejecta masses and velocities from a range of binary neutron star merger simulations encompassing different numerical techniques, various equations of state, binary binary mass ratios $q=0.65-1$, effects of neutrinos and magnetic fields, together with the corresponding ejecta parameters inferred from the ‘blue’ and ‘red’ kilonova of GW170817. Image reproduced with permission from Siegel (2019)

Fig. 6

Longer-lived remnants produce higher $Y_e$ disk wind ejecta and bluer kilonovae. Shown here is the mass distribution by electron fraction $Y_e$ of the disk wind ejecta, calculated for different assumptions about the lifetime, $t_{\mathrm{collapse}}$, of the central NS remnant prior to BH formation, from the axisymmetric $\alpha$-viscosity hydrodynamical calculations of Metzger and Fernández (2014). A vertical line approximately delineates the ejecta with enough neutrons to synthesize lanthanide elements ($Y_e\lesssim 0.25$) generate a red kilonova from that with $Y_e\gtrsim 0.25$ which is lanthanide-poor and will generate blue kilonova emission. The NS lifetime has a strong effect on the ejecta composition because it is a strong source of electron neutrinos, which convert neutrons in the disk to protons via the process ${\nu }_e+n\to p+e^{-}$. This figure is modified from a version in Lippuner et al. (2017)

Fig. 7

Different components of the ejecta from NS–NS mergers and the possible dependence of their kilonova emission on the observer viewing angle, ${\theta }_{\mathrm{obs}}$, relative to the binary axis, in the case of a relatively prompt BH formation (left panel) and a long-lived magnetar remnant (right panel). In both cases, the dynamical ejecta in the equatorial plane is highly neutron-rich ($Y_e\lesssim 0.1$), producing lanthanides and correspondingly “red” kilonova emission peaking at NIR wavelengths. Mass ejected dynamically in the polar directions may be sufficiently neutron-poor ($Y_e\gtrsim 0.3$) to preclude lanthanide production, powering “blue” kilonova emission at optical wavelengths (although this component may be suppressed if BH formation is extremely prompt). The outermost layers of the polar ejecta may contain free neutrons, the decay of which powers a UV transient lasting a few hours following the merger (Sect. 6.1.1). Re-heating of the ejecta by a delayed relativistic outflow (e.g., the GRB jet or a wind from the magnetar remnant) may also contribute to early blue emission (Sect. 6.1.2). The innermost ejecta layers originate from accretion disk outflows, which may emerge more isotropically. When BH formation is prompt, the disk wind ejecta is mainly neutron-rich, powering red kilonova emission (Fernández and Metzger ; Just et al. ; Wu et al. ; Siegel and Metzger 2017). If the NS remnant is instead long-lived relative to the disk lifetime, then neutrino emission can increase $Y_e$ sufficiently to suppress lanthanide production and result in blue disk wind emission (Fig. 6; e.g., Metzger and Fernández ; Perego et al. 2014). Energy input from the central accreting BH or magnetar remnant enhance the kilonova luminosity compared to that exclusively from radioactivity (Sect. 6.2)

Fig. 8

Schematic illustration of the opacity of the NS merger ejecta as a function of photon energy at a fixed epoch near peak light. The free-free opacity (red line) is calculated assuming singly-ionized ejecta of temperature $T=2\times {10}^4$ K and density $\rho ={10}^{-14}$ g ${\text{cm}}^{-3}$, corresponding to the mean properties of ${10}^{-2}{M}_{\odot }$ of ejecta expanding at $v=0.1$ c at $t=$ 3 days. Line opacities of iron-like elements and lanthanide-rich elements are approximated from Figs. 3 and 7 of Kasen et al. (2013). Bound-free opacities are estimated as that of neutral iron (Verner et al. 1996), which should crudely approximate the behavior of heavier r-process elements. Electron scattering opacity accounts for the Klein–Nishina suppression at energies $\gg m_e{c}^2$ and (very schematically) for the rise in opacity that occurs above the keV energy scale due to all electrons (including those bound in atoms) contributing to the scattering opacity when the photon wavelength is smaller than the atomic scale. At the highest energies, opacity is dominated by pair creation by gamma-rays interacting with the electric fields of nuclei in the ejecta (shown schematically for Xenon, $A=131$, $Z=54$). Not included are possible contributions from r-process dust; or $\gamma -\gamma$ pair creation opacity at photon energies $\gg m_e{c}^2\sim {10}^6$ eV (see Eq. 9)

Fig. 9

Kilonova light curves in AB magnitudes for a source at 100 Mpc, calculated using the toy model presented in Sect. 4, assuming a total ejecta mass $M={10}^{-2}{M}_{\odot }$, minimum velocity $v_0=0.1$ c, and gray opacity $\kappa =20{\text{cm}}^2{\text{g}}^{-1}$. The left panel shows a standard “red” kilonova, corresponding to ejecta bearing lanthanide elements, while the right panel shows a “blue” kilonova poor in lanthanides ($\kappa =1{\text{cm}}^2{\text{g}}^{-1}$). Shown for comparison in the red kilonova case with dashed lines are models from Barnes et al. (2016) for $v=0.1$ c and $M={10}^{-2}{M}_{\odot }$. Depending on the relative speeds of the two components and the viewing angle of the observer, both red and blue emission components can be present in a single merger, originating from distinct portions of the ejecta (Fig. 7)

Fig. 10

Bolometric luminosity of the kilonova AT2017gfo associated with GW170817 from Smartt et al. (2017) with uncertainties derived from the range given in the literature (Smartt et al. ; Waxman et al. ; Cowperthwaite et al. ; Arcavi 2018). Also shown are lower limits (empty triangles) on the late-time luminosity as inferred from the Ks band with VLT/HAWK-I (Tanvir et al. 2017) (black) and the 4.5 $\mathrm{\mu }$m detections by the Spitzer Space Telescope from Villar et al. (, green) and (Kasliwal et al. , blue). Colored lines show the ejecta heating rate for models with different values for the ejecta mass and average electron fraction as follows: A ($Y_e=0.15$; $M_{\mathrm{ej}}=0.04M_{\odot }$), B ($Y_e=0.25$; $M_{\mathrm{ej}}=0.04M_{\odot }$), C ($Y_e=0.35$; $M_{\mathrm{ej}}=0.055M_{\odot }$), D ($Y_e=0.45$; $M_{\mathrm{ej}}=0.03M_{\odot }$). While models $A-D$ assume the FRDM nuclear mass model (Möller et al. 1995), Model A1 ($Y_e=0.15$; $M_{\mathrm{ej}}=0.02M_{\odot }$) uses the DZ31 nuclear mass model (Duflo and Zuker 1995). Their corresponding r-process abundance distributions at t = 1 days are shown in the inset. Thermalization is calculated following (Kasen and Barnes 2019) for an assumed ejecta velocity 0.1 c. The black solid (dashed) horizontal lines in the lower right corner represent the approximate observation limits of the NIR (MIR) instruments on the James Webb Space Telescope for a merger at 100 Mpc. Image reproduced with permission from Wu et al. (2019b), copyright by APS

Fig. 11

UVOIR light curves of AT2017gfo from the data set compiled, along with a best-fit spherically symmetric three-component kilonova model (see text). The data in this figure was originally presented in (Andreoni et al. ; Arcavi et al. ; Coulter et al. ; Cowperthwaite et al. ; Díaz et al. ; Drout et al. ; Evans et al. ; Hu et al. ; Kasliwal et al. ; Lipunov et al. ; Pian et al. ; Shappee et al. ; Smartt et al. ; Tanvir et al. ; Troja et al. ; Utsumi et al. ; Valenti et al. 2017). Image reproduced with permission from Villar et al. (2017), copyright by the authors

Fig. 12

Bolometric kilonova light curve during the first few hours of a NS–NS merger, calculated for several model assumptions that can reproduce the measured luminosity $L_{\mathrm{bol}}\approx {10}^{42}$ erg ${\text{s}}^{-1}$ of AT2017gfo at $t\approx 11$ hr (blue uncertainty bar; e.g., Arcavi et al. ; Cowperthwaite et al. ; Drout et al. 2017). Black solid lines show how r-process only models change with the assumed timescale $t_0=0.01,0.1,1$ s at which the outer ejecta was last “thermalized”, i.e. endowed with an internal thermal energy comparable to its asymptotic kinetic energy (at $t\gtrsim t_0$, the ejecta is heated is solely by r-process radioactivity in these models). A small value of $t_0\sim 0.01$ s corresponds to a dynamical ejecta origin with no additional heating, while a large value of $t_0\sim 0.01-1$ s represents the case of a long-lived engine (GRB jet, magnetar wind or accretion disk outflow) which re-heats the ejecta on a timescale $\sim t_0$. We adopt parameters $\beta =3$, $v_0=0.25\text{c}$, $M=0.025M_{\odot }$, $\kappa =0.5{\text{cm}}^2{\text{g}}^{-1}$ (except for the $t_0=1$ s case, for which $M=0.015M_{\odot }$). Red dashed lines show models with $t_0=0.01$ s but for which the outer layer of mass $M_n$ is assumed to contains free neutrons instead of r-process nuclei (a model similar to those shown in Fig. 14). Note that the early-time signatures of neutron decay are largely degenerate with late-time shock re-heating of the ejecta. Image reproduced with permission from Metzger et al. (2018), copyright by the authors

Fig. 13

The four possible outcomes of a NS–NS merger depend on the total binary mass relative to various threshold masses, each of which is proportional to the maximum mass, $M_{\mathrm{TOV}}$, of a non-rotating NS (Table 3). Prompt BH formation or a short-lived HMNS results generates ejecta with a relatively low kinetic energy $\sim {10}^{50}-{10}^{51}$ erg (energy stored in the differential rotation of the HMNS remnant can largely be dissipated as heat and thus lost to neutrinos). By contrast, the delayed formation of a BH through spin-down of a SMNS or stable remnant takes place over longer, secular timescales and must be accompanied by the release of substantial rotational energy $\sim {10}^{52}-{10}^{53}$ erg. Unless effectively “hidden” through GW emission, a large fraction of this energy will be transferred to the ejecta kinetic energy (and, ultimately, the ISM forward shock), thus producing a more luminous kilonova and synchrotron afterglow than for a short-lived remnant Figure credit: Ben Margalit

Fig. 14

Kilonova light curves, including the presence of free neutrons in the outer $M_{\mathrm{n}}={10}^{-4}{M}_{\odot }$ mass layers of the ejecta (“neutron precusor” emission), calculated for the same parameters of total ejecta mass $M={10}^{-2}{M}_{\odot }$ and velocity $v_0=0.1$ c used in Fig. 9. The left panel shows a calculation with an opacity appropriate to lanthanide-bearing nuclei, while the right panel shows an opacity appropriate to lanthanide-free ejecta. Models without a free neutron layer ($M_{\mathrm{n}}=0$; Fig. 9) are shown for comparison with dashed lines

Fig. 15

Kilonova light curves powered by fall-back accretion, calculated for the same parameters of total ejecta mass $M={10}^{-2}{M}_{\odot }$ and velocity $v_0=0.1$ c used in Fig. 9, shown separately assuming opacities appropriate to lanthanide-bearing ($\kappa =20{\text{cm}}^2{\text{g}}^{-1}$; left panel) and lanthanide-free ($\kappa =1{\text{cm}}^2{\text{g}}^{-1}$; right panel) ejecta. We adopt ejecta heating rate following Eq. (34) for a constant efficiency ${ϵ}_{\mathrm{j}}=0.1$ and have normalized the fall-back mass to an optimistic value ${\dot{M}}_{\mathrm{fb}}(t=0.1)={10}^{-2}{M}_{\odot }$ ${\text{s}}^{-1}$

Fig. 16

Kilonova light curves, boosted by spin-down energy from an indefinitely stable magnetar ($t_{\mathrm{collapse}}=\infty$), and taking an opacity $\kappa =20{\text{cm}}^2{\text{g}}^{-1}$ appropriate to lanthanide-rich matter. We assume an ejecta mass $M=0.1M_{\odot }$ (Metzger and Fernández 2014), initial magnetar spin period $P_0=0.7$ ms, thermalization efficiency ${ϵ}_{\mathrm{th}}=1$ and magnetic dipole field strength of ${10}^{15}$ G (left panel) or ${10}^{16}$ G (right panel). Dashed lines show for comparison the purely r-process powered case

Fig. 17

Same as Fig. 16, but calculated for an ejecta opacity $\kappa =1{\text{cm}}^2{\text{g}}^{-1}$ relevant to lanthanide-free matter

Fig. 18

Schematic illustration mapping different types of mergers and their outcomes to trends in their kilonova light curves. The top panel shows the progenitor system, either an NS–NS or an NS–BH binary, while the middle plane shows the final merger remnant (from left to right: an HMNS that collapses to a BH after time $t_{\mathrm{collapse}}$, a spinning magnetized NS, a non-spinning BH and a rapidly spinning BH). The bottom panel illustrates the relative amount of UV/blue emission from an neutron precursor (purple), optical emission from lanthanide-free material (blue) and IR emission from lanthanide containing ejecta (red). Note: the case of a NS–NS merger leading to a slowly spinning black hole is unlikely, given that at a minimum the remnant will acquire the angular momentum of the original binary orbit. Modified from a figure originally presented in Kasen et al. (2015), copyright by the authors