Multiset sparse partial least squares path modeling for high dimensional omics data analysis

Abstract

Background: Recent technological developments have enabled the measurement of a plethora of biomolecular data from various omics domains, and research is ongoing on statistical methods to leverage these omics data to better model and understand biological pathways and genetic architectures of complex phenotypes. Current reviews report that the simultaneous analysis of multiple (i.e. three or more) high dimensional omics data sources is still challenging and suitable statistical methods are unavailable. Often mentioned challenges are the lack of accounting for the hierarchical structure between omics domains and the difficulty of interpretation of genomewide results. This study is motivated to address these challenges. We propose multiset sparse Partial Least Squares path modeling (msPLS), a generalized penalized form of Partial Least Squares path modeling, for the simultaneous modeling of biological pathways across multiple omics domains. msPLS simultaneously models the effect of multiple molecular markers, from multiple omics domains, on the variation of multiple phenotypic variables, while accounting for the relationships between data sources, and provides sparse results. The sparsity in the model helps to provide interpretable results from analyses of hundreds of thousands of biomolecular variables.

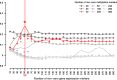
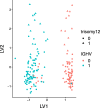
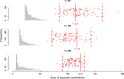
Results: With simulation studies, we quantified the ability of msPLS to discover associated variables among high dimensional data sources. Furthermore, we analysed high dimensional omics datasets to explore biological pathways associated with Marfan syndrome and with Chronic Lymphocytic Leukaemia. Additionally, we compared the results of msPLS to the results of Multi-Omics Factor Analysis (MOFA), which is an alternative method to analyse this type of data.

Conclusions: msPLS is an multiset multivariate method for the integrative analysis of multiple high dimensional omics data sources. It accounts for the relationship between multiple high dimensional data sources while it provides interpretable results through its sparse solutions. The biomarkers found by msPLS in the omics datasets can be interpreted in terms of biological pathways associated with the pathophysiology of Marfan syndrome and of Chronic Lymphocytic Leukaemia. Additionally, msPLS outperforms MOFA in terms of variation explained in the chronic lymphocytic leukaemia dataset while it identifies the two most important clinical markers for Chronic Lymphocytic Leukaemia AVAILABILITY: http://uva.csala.me/mspls.https://github.com/acsala/2018_msPLS.

Keywords: High dimensional omics data; Multivariate analysis; Partial least squares.

Fig. 1

msPLS identified a combination of 40 epigenomic markers (denoted as ξ₁) and 52 transcriptomic markers (denoted as ξ₂) that explain the most variance in the proteome variables. The color scale represents the strength of w regression weights

Fig. 2

msPLS identified 40 methylation markers and 52 gene expression markers that optimised the sum of squared correlation of the explanatory LVs of the epigenome and transcriptome with the MVs from the proteome

Fig. 3

The resulting model from Section 3.2 extended to two LVs per dataset. The first set of LVs ξ₁₍₁₎ and ξ₂₍₁₎ partition out a different portion of variance in the proteome MVs than the second set of LVs ξ₁₍₂₎ and ξ₂₍₂₎. The colour scale represents the strength of w regression weights

Fig. 4

The co-expression pattern of the resulting Marfan genes queried on their biological process based functions. The figure was produced with GeneMania (available at https://genemania.org)

Fig. 5

The samples of the CLL data clustered around on their IGHV and trisomy 12 status, extracted by the first and second LV of the msPLS model. The figure was produced by the MOFA R package [11]

Fig. 6

The proposed relationship between three data sources. X₁ and X₂ have a symmetric relation (i.e. they are responses for each other) and X₃ have asymmetric relation with both X₁ and X₂ (i.e. X₃ is response for both X₂ and X₁)

Fig. 7

The null distributions of the optimisation criteria (with respect to X₃) for the simulated data with different sample sizes (n = 50, 100, 250), obtained after 1000 permutations. The red bars indicate the optimisation criteria obtained applying msPLS to the original data with the optimal λ₁ parameters for UST. The red dots are the bootstrapped values, and the dashed red bars are the 95% confidence intervals