A distributional code for value in dopamine-based reinforcement learning
- PMID: 31942076
- PMCID: PMC7476215
- DOI: 10.1038/s41586-019-1924-6
A distributional code for value in dopamine-based reinforcement learning
Abstract
Since its introduction, the reward prediction error theory of dopamine has explained a wealth of empirical phenomena, providing a unifying framework for understanding the representation of reward and value in the brain1-3. According to the now canonical theory, reward predictions are represented as a single scalar quantity, which supports learning about the expectation, or mean, of stochastic outcomes. Here we propose an account of dopamine-based reinforcement learning inspired by recent artificial intelligence research on distributional reinforcement learning4-6. We hypothesized that the brain represents possible future rewards not as a single mean, but instead as a probability distribution, effectively representing multiple future outcomes simultaneously and in parallel. This idea implies a set of empirical predictions, which we tested using single-unit recordings from mouse ventral tegmental area. Our findings provide strong evidence for a neural realization of distributional reinforcement learning.
Conflict of interest statement
Competing Interests
The authors declare that they have no competing financial interests.
Figures
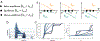



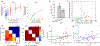





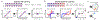
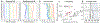
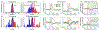

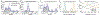
Comment in
-
Reinforcement Learning: Full Glass or Empty - Depends Who You Ask.Curr Biol. 2020 Apr 6;30(7):R321-R324. doi: 10.1016/j.cub.2020.02.062. Curr Biol. 2020. PMID: 32259508
-
Beyond the Average View of Dopamine.Trends Cogn Sci. 2020 Jul;24(7):499-501. doi: 10.1016/j.tics.2020.04.006. Epub 2020 May 15. Trends Cogn Sci. 2020. PMID: 32423707 Free PMC article.
References
-
- Schultz Wolfram, Wiliam R Stauffer, and Armin Lak. The phasic dopamine signal maturing: from reward via behavioural activation to formal economic utility. Current opinion in neurobiology, 43: 139–148, 2017. - PubMed
-
- Morimura Tetsuro, Sugiyama Masashi, Kashima Hisashi, Hachiya Hirotaka, and Tanaka Toshiyuki. Parametric return density estimation for reinforcement learning In Proceedings of the Twenty-Sixth Conference on Uncertainty in Artificial Intelligence, UAI’10, pages 368–375, Arlington, Virginia, United States, 2010. AUAI Press; ISBN 978-0-9749039-6-5. URL http://dl.acm.org/citation.cfm?id=3023549.3023592.
-
- Marc G Bellemare Will Dabney, and Munos Rémi. A distributional perspective on reinforcement learning. In International Conference on Machine Learning, pages 449–458, 2017.
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

