Mix and Match: Phenotypic Coexistence as a Key Facilitator of Cancer Invasion

Abstract

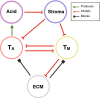
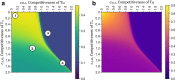
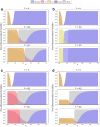
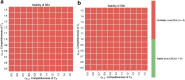
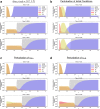
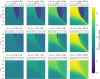
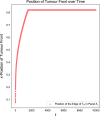
Invasion of healthy tissue is a defining feature of malignant tumours. Traditionally, invasion is thought to be driven by cells that have acquired all the necessary traits to overcome the range of biological and physical defences employed by the body. However, in light of the ever-increasing evidence for geno- and phenotypic intra-tumour heterogeneity, an alternative hypothesis presents itself: could invasion be driven by a collection of cells with distinct traits that together facilitate the invasion process? In this paper, we use a mathematical model to assess the feasibility of this hypothesis in the context of acid-mediated invasion. We assume tumour expansion is obstructed by stroma which inhibits growth and extra-cellular matrix (ECM) which blocks cancer cell movement. Further, we assume that there are two types of cancer cells: (i) a glycolytic phenotype which produces acid that kills stromal cells and (ii) a matrix-degrading phenotype that locally remodels the ECM. We extend the Gatenby-Gawlinski reaction-diffusion model to derive a system of five coupled reaction-diffusion equations to describe the resulting invasion process. We characterise the spatially homogeneous steady states and carry out a simulation study in one spatial dimension to determine how the tumour develops as we vary the strength of competition between the two phenotypes. We find that overall tumour growth is most extensive when both cell types can stably coexist, since this allows the cells to locally mix and benefit most from the combination of traits. In contrast, when inter-species competition exceeds intra-species competition the populations spatially separate and invasion arrests either: (i) rapidly (matrix-degraders dominate) or (ii) slowly (acid-producers dominate). Overall, our work demonstrates that the spatial and ecological relationship between a heterogeneous population of tumour cells is a key factor in determining their ability to cooperate. Specifically, we predict that tumours in which different phenotypes coexist stably are more invasive than tumours in which phenotypes are spatially separated.

Keywords: Coexistence theory; Cooperation; Reaction–diffusion; Travelling waves; Tumour invasion.

Fig. 1

Areas of acid production and matrix remodelling in human breast cancer ducts. Acid production was defined by expression of the acid adaptation marker LAMP2 (green). Matrix remodelling was defined by expression of TGM2 (purple). For visualisation purposes, masks were extracted and overlaid on a haematoxylin and eosin stain of the same tissue (see Section A1 for details). a Example of a ductal carcinoma in situ that has not yet invaded the surrounding tissue. b Example of an invasive cancer that has breached the duct. We observe that not all cells are expressing LAMP2 or TGM2. Could there be cooperation between cells with different traits? (Color figure online)

Fig. 2

Interaction diagram of our model. Stroma inhibits tumour cell proliferation but is killed by acid secreted by the acid producing tumour cells, $T_{\mathrm{A}}$. In contrast, tumour cells ($T_{\mathrm{A}}$ and $T_{\mathrm{M}}$) are assumed to be resilient to acid. ECM blocks movement of the tumour cells, but can be removed by the matrix-degrading tumour cells, $T_{\mathrm{M}}$. The two types of tumour cells compete for resources thereby inhibiting each other’s growth (Color figure online)

Fig. 3

In isolation, the tumour populations fail to invade. a Snapshots at three time points from a long-term simulation ($t_{\text{end}}=10,000$, corresponding to more than 10 years) in which only $T_{\mathrm{A}}$ is present. Expansion stalls because of obstruction by the matrix. b Analogous simulation of the dynamics with $T_{\mathrm{M}}$ in isolation. This time the tumour cannot overcome the stroma. c Plot showing the position of the tumour edge in Panels A and B over time, determined as ${min}_{x\in [0,1]}\left\{\text{d},/,\text{d},t,(,T_i,(t),)\right\}$ for $i=\text{A},\text{M}$, respectively. We conclude that the model and the numerical scheme behave as expected and that any invasion seen later in this paper is due to the interaction between the two cell types (Colour figure online)

Fig. 4

The invasive potential of a tumour is determined by the competition between its subpopulations. a Position of the tumour front at time $t=50$ (575 days) as a function of the strength of inter-species competition ($c_{\mathrm{M},\mathrm{A}}$ and $c_{\mathrm{A},\mathrm{M}}$). This was defined as $max(x_{\mathrm{A}},x_{\mathrm{M}})$, where $x_i={min}_{x\in [0,1]}\left\{\text{d},/,\text{d},t,(,T_i,(50),)\right\}$ for $i=$ A or M, respectively, is the position of the wave front of $T_{\mathrm{A}}$ and $T_{\mathrm{M}}$ at time 50. Annotations (numbers in circles) correspond to the time-series plots as shown in Fig. 5. We find the tumour advances furthest when inter-species competition is weaker than intra-species competition ($c_{\mathrm{M},\mathrm{A}},c_{\mathrm{A},\mathrm{M}}<1$). As the strength of inter-species competition increases above that of intra-species competition ($c_{\mathrm{M},\mathrm{A}},c_{\mathrm{A},\mathrm{M}}>1$), invasion slows, especially if $T_{\mathrm{M}}$ dominates. b Total tumour mass, defined as $\mathcal{M}={\int }_{x=0}^1{T}_{\mathrm{A}}(x,50)+T_{\mathrm{M}}(x,50)\text{d}x$, as a function of the inter-species competition. We see that the total tumour mass in the invading tumour, which may be interpreted as a proxy for the total cell number, is a strictly and rapidly decreasing function of the competition parameters. Thus, competition between tumour cells influences not only how far they invade, but also how many cells make up the advancing tumour. Note: cases in which the cell populations were small (${\int }_{x=0}^1{T}_i(x,50)\text{d}x<0.1$) were disregarded in this analysis to avoid issues associated with the simulation and interpretation of low densities (Colour figure online)

Fig. 5

Simulations illustrating the four different scenarios that can occur depending on the inter-species competition between $T_{\mathrm{A}}$ and $T_{\mathrm{M}}$. Panels correspond to the locations in the competition parameter space marked in Fig. 4a (1:A, 2:B, 3:C, 4:D). a$(c_{\mathrm{M},\mathrm{A}},c_{\mathrm{A},\mathrm{M}})=(0,0)$. At $t=0$, the tumour begins as a mixture of acid-producing (red) and matrix-degrading cells (yellow) on the left-hand side of the domain (appearing orange due to the mixture of the colours). It is constrained by a mixture of stroma (blue) and ECM (grey) on the right-hand side (appearing as dark blue). Since inter-species competition is weak, the tumour populations can coexist and combine their traits, allowing them to invade rapidly ($t=25$ and $t=50$). b$(c_{\mathrm{M},\mathrm{A}},c_{\mathrm{A},\mathrm{M}})=(1.2,0.7)$. In contrast, when $T_{\mathrm{M}}$ dominates over $T_{\mathrm{A}}$, it drives $T_{\mathrm{A}}$ to extinction and no invasion takes place. c$(c_{\mathrm{M},\mathrm{A}},c_{\mathrm{A},\mathrm{M}})=(0.7,1.2)$. $T_{\mathrm{A}}$ dominates over $T_{\mathrm{M}}$. While invasion eventually stops due to a lack of ECM degradation, the tumour initially invades thanks to a small population of $T_{\mathrm{M}}$ persisting at the tumour edge (appearing in orange at $t=25$). d$(c_{\mathrm{M},\mathrm{A}},c_{\mathrm{A},\mathrm{M}})=(1.7,1.7)$. Mutual exclusion of $T_{\mathrm{A}}$ and $T_{\mathrm{M}}$. When seeded at equal densities, the two populations will invade as shown, but the invading front is not stable. If a small perturbation is introduced, the two populations will separate and invasion will halt (Fig. 8)

Fig. 6

Summary of the key findings of this paper. If the two phenotypes can coexist, a highly invasive community of cells emerges. Conversely, if $T_{\mathrm{M}}$ dominates, tumour invasion comes to a halt as the cells are unable to overcome the stroma. If $T_{\mathrm{A}}$ dominates, then a temporarily invasive tumour mass forms in which $T_{\mathrm{M}}$ cells find a temporary habitat in the matrix at the tumour edge. Finally, in the case where the two cell types mutually exclude each other’s growth, the cells separate into spatially distinct regions and fail to invade (Colour figure online)

Fig. 7

Numerical stability analysis of SS4 (a) and SS6 (b) for the range of parameters considered in this paper (see Table 1). Stability was assessed by computing the eigenvalues of the Jacobian at the steady state and assessing whether at least one eigenvalue had a strictly positive real part. We find that both SS4 and SS6 are unstable across the range of parameters considered (Color figure online)

Fig. 8

Instability of the invasive front when $c_{\mathrm{M},\mathrm{A}}=c_{\mathrm{A},\mathrm{M}}$. a Simulation for $c_{\mathrm{M},\mathrm{A}}=c_{\mathrm{A},\mathrm{M}}=1.7$. b Perturbation of the initial conditions in a. The initial distribution of $T_{\mathrm{M}}$ was shifted by $\delta x=0.15$ to the right, resulting in subsequent spatial separation of the two phenotypes and arresting of invasion. c Small perturbation in $c_{\mathrm{M},\mathrm{A}}$ ($(c_{\mathrm{M},\mathrm{A}},c_{\mathrm{A},\mathrm{M}})=(1.700001,1.7)$). d Small perturbation in $c_{\mathrm{A},\mathrm{M}}$ ($(c_{\mathrm{M},\mathrm{A}},c_{\mathrm{A},\mathrm{M}})=(1.7,1.700001)$). This indicates that the system is structurally unstable in this parameter regime (Colour figure online)

Fig. 9

Sensitivity analysis for the parameters $c_{\mathrm{M},\mathrm{A}},c_{\mathrm{A},\mathrm{M}},c_S$, and $\kappa$. Each heatmap shows the position of the front of the tumour at $t=50$ (computed as for Fig. 4a) (Colour figure online)

Fig. 10

When $T_{\mathrm{A}}$ drives $T_{\mathrm{M}}$ to extinction, only transient invasion occurs. Position of the tumour edge simulated until $t=10,000$ for $(c_{\mathrm{M},\mathrm{A}},c_{\mathrm{A},\mathrm{M}})=(0.5,1.5)$. The tumour transiently advances, while the $T_{\mathrm{M}}$ initially persists. However, eventually $T_{\mathrm{M}}$ is eradicated and invasion stalls