Whitening of odor representations by the wiring diagram of the olfactory bulb
- PMID: 31959937
- PMCID: PMC7101160
- DOI: 10.1038/s41593-019-0576-z
Whitening of odor representations by the wiring diagram of the olfactory bulb
Abstract
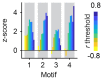
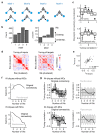
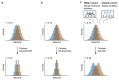
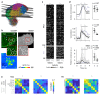
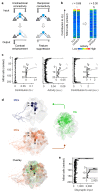
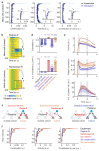
Neuronal computations underlying higher brain functions depend on synaptic interactions among specific neurons. A mechanistic understanding of such computations requires wiring diagrams of neuronal networks. In this study, we examined how the olfactory bulb (OB) performs 'whitening', a fundamental computation that decorrelates activity patterns and supports their classification by memory networks. We measured odor-evoked activity in the OB of a zebrafish larva and subsequently reconstructed the complete wiring diagram by volumetric electron microscopy. The resulting functional connectome revealed an over-representation of multisynaptic connectivity motifs that mediate reciprocal inhibition between neurons with similar tuning. This connectivity suppressed redundant responses and was necessary and sufficient to reproduce whitening in simulations. Whitening of odor representations is therefore mediated by higher-order structure in the wiring diagram that is adapted to natural input patterns.
Conflict of interest statement
A.A.W. is the founder and owner of ariadne-service.
Figures

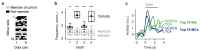



References
-
- Simoncelli EP, Olshausen BA. Natural image statistics and neural representation. Annu Rev Neurosci. 2001;24:1193–1216. - PubMed
-
- Bishop CM. Neural networks for pattern recognition. Clarendon Press; Oxford: 1995.
-
- Barlow HB. In: Sensory communication. Rosenblith WA, editor. MIT Press; 1961. pp. 217–234.
-
- Atick JJ, Redlich AN. Convergent algorithm for sensory receptive-field development. Neural Comput. 1993;5:45–60.
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Molecular Biology Databases
Research Materials
Miscellaneous

