Mice adaptively generate choice variability in a deterministic task
- PMID: 31965053
- PMCID: PMC6972896
- DOI: 10.1038/s42003-020-0759-x
Mice adaptively generate choice variability in a deterministic task
Erratum in
-
Author Correction: Mice adaptively generate choice variability in a deterministic task.Commun Biol. 2020 Jan 31;3(1):54. doi: 10.1038/s42003-020-0785-8. Commun Biol. 2020. PMID: 32005936 Free PMC article.
Abstract
Can decisions be made solely by chance? Can variability be intrinsic to the decision-maker or is it inherited from environmental conditions? To investigate these questions, we designed a deterministic setting in which mice are rewarded for non-repetitive choice sequences, and modeled the experiment using reinforcement learning. We found that mice progressively increased their choice variability. Although an optimal strategy based on sequences learning was theoretically possible and would be more rewarding, animals used a pseudo-random selection which ensures high success rate. This was not the case if the animal is exposed to a uniform probabilistic reward delivery. We also show that mice were blind to changes in the temporal structure of reward delivery once they learned to choose at random. Overall, our results demonstrate that a decision-making process can self-generate variability and randomness, even when the rules governing reward delivery are neither stochastic nor volatile.
Conflict of interest statement
The authors declare no competing interests.
Figures

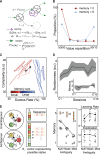
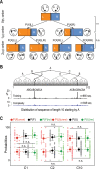
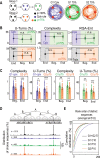
References
-
- Driver, P. M. & Humphries, D. A. Protean behaviour. (Oxford University Press, USA, 1988).
-
- Rapoport A, Budescu DV. Generation of random series in two-person strictly competitive games. J. Exp. Psychol. Gen. 1992;121:352–363. doi: 10.1037/0096-3445.121.3.352. - DOI
-
- Sutton, R. S. & Barto, A. G. Reinforcement Learning. (MIT Press, 1998).
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources

