A general method to generate artificial spike train populations matching recorded neurons
- PMID: 31974719
- PMCID: PMC7036336
- DOI: 10.1007/s10827-020-00741-w
A general method to generate artificial spike train populations matching recorded neurons
Abstract
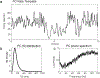
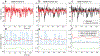
We developed a general method to generate populations of artificial spike trains (ASTs) that match the statistics of recorded neurons. The method is based on computing a Gaussian local rate function of the recorded spike trains, which results in rate templates from which ASTs are drawn as gamma distributed processes with a refractory period. Multiple instances of spike trains can be sampled from the same rate templates. Importantly, we can manipulate rate-covariances between spike trains by performing simple algorithmic transformations on the rate templates, such as filtering or amplifying specific frequency bands, and adding behavior related rate modulations. The method was examined for accuracy and limitations using surrogate data such as sine wave rate templates, and was then verified for recorded spike trains from cerebellum and cerebral cortex. We found that ASTs generated with this method can closely follow the firing rate and local as well as global spike time variance and power spectrum. The method is primarily intended to generate well-controlled spike train populations as inputs for dynamic clamp studies or biophysically realistic multicompartmental models. Such inputs are essential to study detailed properties of synaptic integration with well-controlled input patterns that mimic the in vivo situation while allowing manipulation of input rate covariances at different time scales.
Keywords: Cerebellum; Correlation; Cortex; In vivo; Model; Synaptic.
Figures
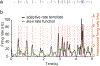






References
-
- Abeles M (1983). The quantification and graphic display of correlations among three spike trains. IEEE.Trans.Biomed.Eng BME-30, 235–239. - PubMed
-
- Aertsen A, Diesmann M, & Gewaltig MO (1996). Propagation of synchronous spiking activity in feedforward neural networks. J.Physiol.(Paris.) 90, 243–247. - PubMed
-
- Allers KA, Ruskin DN, Bergstrom DA, Freeman LE, Ghazi LJ, Tierney PL, & Walters JR (2002). Multisecond periodicities in basal ganglia firing rates correlate with theta bursts in transcortical and hippocampal EEG. J.Neurophysiol 87, 1118–1122. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources

