Thermal fracture kinetics of heterogeneous semiflexible polymers

Abstract

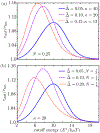
The fracture and severing of polymer chains plays a critical role in the failure of fibrous materials and the regulated turnover of intracellular filaments. Using continuum wormlike chain models, we investigate the fracture of semiflexible polymers via thermal bending fluctuations, focusing on the role of filament flexibility and dynamics. Our results highlight a previously unappreciated consequence of mechanical heterogeneity in the filament, which enhances the rate of thermal fragmentation particularly in cases where constraints hinder the movement of the chain ends. Although generally applicable to semiflexible chains with regions of different bending stiffness, the model is motivated by a specific biophysical system: the enhanced severing of actin filaments at the boundary between stiff bare regions and mechanically softened regions that are coated with cofilin regulatory proteins. The results presented here point to a potential mechanism for disassembly of polymeric materials in general and cytoskeletal actin networks in particular by the introduction of locally softened chain regions, as occurs with cofilin binding.

Figure 1.

Model schematic and energy landscapes. (a) Lowest energy (athermal) configuration of homogeneous chain with fixed R/(2L) = 0.6 and model parameters labeled. (b) Free energy landscape for homogeneous chain shown in (a), plotted as a function of junction bending and normalized end distance. White line markes the lowest energy path to steeper junction angles. (c) Lowest energy configuration for a heterogeneous chain with fixed R/(2L) = 0.6 and ℓ_p,1/ℓ_p,2 = 10. Light blue segment corresponds to softer chain side. (d) Overall free energy landscape for the heterogeneous chain with h = 10.

Figure 2.

Comparison of approximate dynamics over free energy landscapes versus Brownian dynamics simulations, for homogeneous chains (h = 1). (a) MFPT to a cutoff junction energy E*, for fixed end distance. (b) MFPT to a cutoff value of the normalized end-to-end distance r. (c) MFPT to a junction energy E*, with free chain ends. In all cases, dashed black lines correspond to first passage times calculated from the free energy landscapes, solid lines correspond to Brownian dynamics simulations. All times are non-dimensionalized by $D_{\rho }^{(0)}$. Top panels show examples of start and end configurations, with junction color indicating energy at the junction.

Figure 3.

Chain heterogeneity enhances junction fracture rates when chain end dynamics are slow. (a) Ratio of MFPT to fracture for uniformly stiff (h = 1) and heterogeneous (h = 10) chains is plotted versus the relative rate of chain end dynamics compared to junction dynamics. (b-c) Time to fragmentation in the limit of infinitely slow chain end dynamics. Dimensionless MFPT is shown as a function of heterogeneity h for (b) chains with a fixed junction length $\widehat{\Delta }$ = 0.1 and varying stiffness and (c) chains with a fixed stiffness (N = 0.25) but varying junction length. Chains are assumed to start from an equilibrium distribution.

Figure 4.

Enhancement in fracture rate for a heterogeneous vs homogeneous chain with free chain ends. The ratio of MFPT to fracture for a fully stiff chain (h = 1) vs a heterogeneous chain (h = 10) is plotted as a function of the cutoff energy. (a) Filaments with constant length N but varying junction size and stiffness. (b) Filaments with varying length but constant junction stiffness κ.