Parton distributions from high-precision collider data: NNPDF Collaboration
- PMID: 31997920
- PMCID: PMC6956957
- DOI: 10.1140/epjc/s10052-017-5199-5
Parton distributions from high-precision collider data: NNPDF Collaboration
Abstract
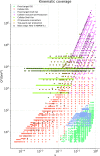
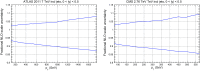
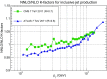
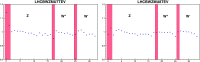
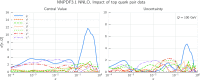
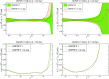
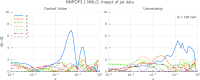
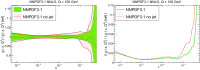
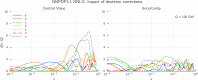
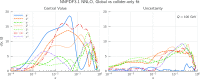
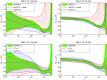
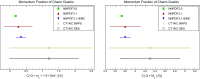
We present a new set of parton distributions, NNPDF3.1, which updates NNPDF3.0, the first global set of PDFs determined using a methodology validated by a closure test. The update is motivated by recent progress in methodology and available data, and involves both. On the methodological side, we now parametrize and determine the charm PDF alongside the light-quark and gluon ones, thereby increasing from seven to eight the number of independent PDFs. On the data side, we now include the D0 electron and muon W asymmetries from the final Tevatron dataset, the complete LHCb measurements of W and Z production in the forward region at 7 and 8 TeV, and new ATLAS and CMS measurements of inclusive jet and electroweak boson production. We also include for the first time top-quark pair differential distributions and the transverse momentum of the Z bosons from ATLAS and CMS. We investigate the impact of parametrizing charm and provide evidence that the accuracy and stability of the PDFs are thereby improved. We study the impact of the new data by producing a variety of determinations based on reduced datasets. We find that both improvements have a significant impact on the PDFs, with some substantial reductions in uncertainties, but with the new PDFs generally in agreement with the previous set at the one-sigma level. The most significant changes are seen in the light-quark flavor separation, and in increased precision in the determination of the gluon. We explore the implications of NNPDF3.1 for LHC phenomenology at Run II, compare with recent LHC measurements at 13 TeV, provide updated predictions for Higgs production cross-sections and discuss the strangeness and charm content of the proton in light of our improved dataset and methodology. The NNPDF3.1 PDFs are delivered for the first time both as Hessian sets, and as optimized Monte Carlo sets with a compressed number of replicas.
© The Author(s) 2017.
Figures

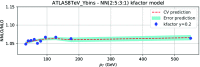

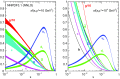
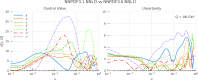

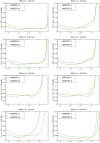




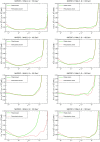

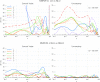
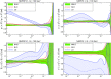
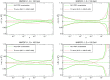

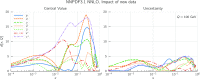

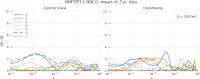

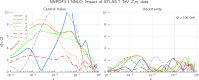
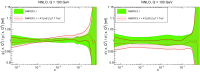


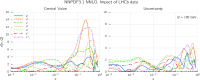

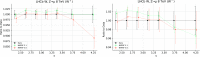
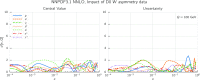

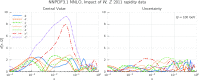
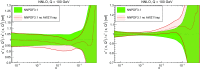
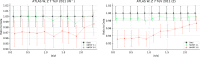

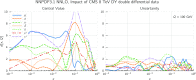

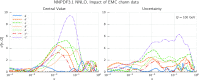

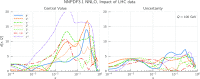

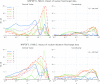
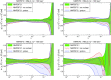
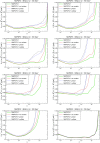




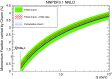
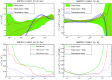
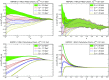
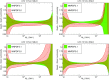
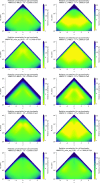
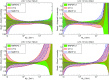
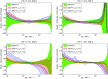
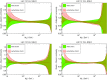





References
-
- Forte S. Parton distributions at the dawn of the LHC. Acta Phys. Polon. B. 2010;41:2859.
-
- Forte S, Watt G. Progress in the determination of the partonic structure of the proton. Annu. Rev. Nucl. Part. Sci. 2013;63:291. doi: 10.1146/annurev-nucl-102212-170607. - DOI
-
- Ball RD. Global Parton distributions for the LHC Run II. Nuovo Cim. 2016;38(4):127.
-
- Rojo J, et al. The PDF4LHC report on PDFs and LHC data: results from Run I and preparation for Run II. J. Phys. G. 2015;42:103103. doi: 10.1088/0954-3899/42/10/103103. - DOI
-
- NNPDF Collaboration, R. D. Ball et al., Parton distributions for the LHC Run II. JHEP 04, 040 (2015). arXiv:1410.8849
LinkOut - more resources
Full Text Sources
