Computer-Controlled Biaxial Bioreactor for Investigating Cell-Mediated Homeostasis in Tissue Equivalents

Abstract

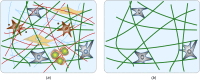
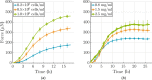
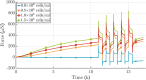
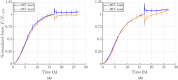
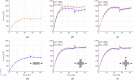
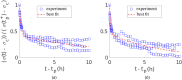
Soft biological tissues consist of cells and extracellular matrix (ECM), a network of diverse proteins, glycoproteins, and glycosaminoglycans that surround the cells. The cells actively sense the surrounding ECM and regulate its mechanical state. Cell-seeded collagen or fibrin gels, so-called tissue equivalents, are simple but powerful model systems to study this phenomenon. Nevertheless, few quantitative studies document the stresses that cells establish and maintain in such gels; moreover, most prior data were collected via uniaxial experiments whereas soft tissues are mainly subject to multiaxial loading in vivo. To begin to close this gap between existing experimental data and in vivo conditions, we describe here a computer-controlled bioreactor that enables accurate measurements of the evolution of mechanical tension and deformation of tissue equivalents under well-controlled biaxial loads. This device allows diverse studies, including how cells establish a homeostatic state of biaxial stress and if they maintain it in response to mechanical perturbations. It similarly allows, for example, studies of the impact of cell and matrix density, exogenous growth factors and cytokines, and different types of loading conditions (uniaxial, strip-biaxial, and biaxial) on these processes. As illustrative results, we show that NIH/3T3 fibroblasts establish a homeostatic mechanical state that depends on cell density and collagen concentration. Following perturbations from this homeostatic state, the cells were able to recover biaxial loading similar to homeostatic. Depending on the precise loads, however, they were not always able to fully maintain that state.

Fig. 1

Schematic of native tissue consisting of various fiber and cell types, as well as additional constituents (a); cell-seeded collagen (Fig. 5(b)) gel as a simplified model system to study cell–matric interactions (b). In both cases, we emphasize the typical multiaxial geometry and loading that is important for in vivo relevance.

Fig. 2

(a) Biaxial bioreactor and mechanical testing device with attached sample and (b) schematic drawing showing the inside of the bath chamber and the load cells mounted from above

Fig. 3

(a) A porous insert for attaching a gel to the testing device; (b) two-part mold having a cruciform shape to form gels; (c) floated cruciform gel attached to testing device; and (d) dog-bone shape mold for uniaxial experiments

Fig. 4

Compaction of a cruciform gel from an initial configuration (solid line at 0 h) to a deformed contour (solid line at 24 h) due to contractile forces imposed by resident cells (dashed line at 24 h indicates initial configuration): (a) freely floating gel and (b) uniaxially constrained gel

Fig. 5

(a) Influence of cell density and (b) collagen concentration on force development in a uniaxial setting (cells were serum-starved; each curve shows the mean ± SEM for three identical experiments). (a) Note that force development depends nonlinearly on cell density: more cells/mL lead to higher forces; (b) force development depends nearly linearly on collagen concentration, higher concentrations lead to higher force.

Fig. 6

Analysis of the effect of 3T3 cell density on force development in case of a ±2.0% stretch alternating every 30 min after an initial 11 h culture period in uniaxial setting. The total force increases when the number of cells increases. Additionally, the amplitude of the resulting force perturbation due to applied stretch is higher for a larger number of cells. Since cells were not treated to prevent proliferation, no plateau in force was reached. The acellular gel shows typical viscoelastic relaxation behavior (collagen concentration 1.5 mg/mL), which differs dramatically from the active relaxation/recovery achieved via cell-mediation. Shown is one experiment for each cell density.

Fig. 7

Influence of amplitude and direction of perturbation: force development was measured for 10 h following a perturbation in loading (uniaxial setting, cells were serum-starved; experiments were force-controlled: 10% load means application of a force that equals 10% of the homeostatic force; each curve shows the mean ± SEM of three identical experiments). (a) Increasing or releasing the load by 10%: a positive perturbation elicited a cell-mediated relaxation toward the prior steady-state force with a small residual offset whereas a negative perturbation resulted in a recovery of the homeostatic force. (b) Conversely increasing load by 20% led to a notable offset from homeostatic force after 10 h of cell-mediated relaxation whereas decreasing load by 20% led to a continuous increase in force, with a new plateau not reached over the subsequent 10 h.

Fig. 8

Influence of boundary conditions on force development prior to and after perturbing the load from steady-state (cells treated with Mitomycin C to minimize cell proliferation during testing; each curve shows the mean±SEM of three identical experiments). First row: 20% reduction in load after an initial 27 h culture period under uniaxial, strip-biaxial, or equi-biaxial ((a)–(c)) conditions. Second row: 20% increase in load after 27 h in uniaxial, strip-biaxial, and equi-biaxial ((d)–(f)) conditions.

Fig. 9

Best fit of Eq. (1) with n = 2 exponentials to stress recovery data (hours 27–37) of uniaxial experiments shown in Figs. 8(a) and 8(d). (a) Decreased load perturbation from the homeostatic state according to Fig. 8(a); (b) increased load perturbation from homeostatic state according to Fig. 8(d).