Four-dimensional micro-building blocks

Abstract

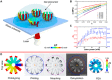
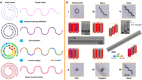
Four-dimensional (4D) printing relies on multimaterial printing, reinforcement patterns, or micro/nanofibrous additives as programmable tools to achieve desired shape reconfigurations. However, existing programming approaches still follow the so-called origami design principle to generate reconfigurable structures by self-folding stacked 2D materials, particularly at small scales. Here, we propose a programmable modular design that directly constructs 3D reconfigurable microstructures capable of sophisticated 3D-to-3D shape transformations by assembling 4D micro-building blocks. 4D direct laser writing is used to print two-photon polymerizable, stimuli-responsive hydrogels to construct building blocks at micrometer scales. Denavit-Hartenberg (DH) parameters, used to define robotic arm kinematics, are introduced as guidelines for how to assemble the micro-building blocks and plan the 3D motion of assembled chain blocks. Last, a 3D-printed microscaled transformer capable of changing its shape from a race car to a humanoid robot is devised and fabricated using the DH parameters to guide the motion of various assembled compartments.

Fig. 1. Spatial and temporal control in direct laser writing to enable spatially controlled differentially cross-linked polymer networks.

(A) Schematic of the printing process using a DLW system. The color bar of the laser power (LP) ranges from 10 to 40 mW. (B) Mechanical characteristics of the printed material with varying laser power, in which σ denotes the nominal compression stress and λ is the corresponding stretch ratio. (C) Effect of laser power on the cross-linking density Nv and the Flory interaction parameter (χ). (D) Flower-like microstructure with programmed responsiveness to demonstrate controllable deformation. The outer (passive) layers of all petals were printed with a laser power of 40 mW and at a scanning speed of 8 mm/s; the inner (active) layer of each petal was printed at the same speed but with gradually increased laser power. After complete dehydration, the transformed petals exhibited the same bending curvature as those predicted by FEA. Scale bar, 40 μm.

Fig. 2. Evolution of 3D-printed building blocks.

(A) 4D micro-building blocks evolve from conventional static 3D-printed building blocks to deformable building blocks and further to articulated building blocks owing to the development of active materials and micromachining techniques. The shrinkage of the active layer mainly drives the deformation during decreasing of the solvent pH, which makes the bilayer structures bend toward the active layer. (B) Effect of the thickness ratio between the active layer and passive layer (m) on the bending curvature (κ), indicating that the articulated building blocks deform more than conventional bilayer building blocks. (C) Bending curvature of the articulated building blocks finely tuned by varying the slenderness ratio (b′) between the width and height of the blocks and the laser parameters between the active and passive layers. (D) Various simulated shape transformation modes of the articulated building blocks by varying the spatial arrangement of the bilayer mechanisms and the compliant hinge joints.

Fig. 3. Design principle and assembly rules of the modular system with the aid of finite element simulations.

(A) Schematics and design geometry of the articulated building blocks whose basic structure is an octagonal prismatic hollow cylinder composed of pairs of active layers, passive layers, and hinge joints. (B) Rotational deformation induced by the shrinking of the active layers. Each building block can be viewed as a combination of a rotational joint and a rigid bar, resembling a robotic arm. (C to E) Schematics of rotational movements with controlled amplitude and orientation enabled by the assembly of various preprogrammed building blocks. (B), (C), (D), and (E) define how the four DH parameters θ, R, d, and α are implemented in our modular building blocks, respectively. FEA provides a means for the quantitative assembly of the complex modular system.

Fig. 4. Inverse and forward design of morphing modular systems.

(A) Inverse problem finding for programming a structure that morphs into the desired shape. Given an arbitrary shape, such as a wave, the modular design converts it to a discrete counterpart with a finite number of joints and then obtains the DH parameters. The modular system subsequently constructs the shape transformation between the given wave shape and an assembled roll configuration by encoding the inversed θ_z into the roll, for it to morph into the shape of a wave. In the image of the inverse design of a roll encoded with different colors, the solid circles indicate that θ_z is positive, and the hollow circles indicate that θ_z is negative. (B) Optical images of the assembled building blocks encoded with different DH parameters.

Fig. 5. 3D assembly of 4D building blocks for constructing a micrometer-scale transformer.

(A) Computer-aided design model of a microscale race car following the proposed assembly rule. The color pink denotes the components that are rigid and nondeformable. (B) 4D DLW design and fabrication of the devised race car. (C) Detailed connections of the five main parts: neck, shoulder, arms, backbone, and legs. (D) Programmed deformation of each compartment encoded with defined DH parameters. (E) Sequential optical images showing the 3D-to-3D shape-morphing process of the microscale transformer from a race car to a humanoid robot. The blue arrow denotes the diffusion direction of acidic fluid flow.