Exploring Protein Fold Space

Abstract

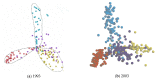
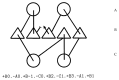
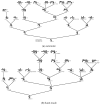
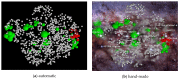
The model of protein folding proposed by Ptitsyn and colleagues involves the accretion of secondary structures around a nucleus. As developed by Efimov, this model also provides a useful way to view the relationships among structures. Although somewhat eclipsed by later databases based on the pairwise comparison of structures, Efimov's approach provides a guide for the more automatic comparison of proteins based on an encoding of their topology as a string. Being restricted to layers of secondary structures based on beta sheets, this too has limitations which are partly overcome by moving to a more generalised secondary structure lattice that can encompass both open and closed (barrel) sheets as well as helical packing of the type encoded by Murzin and Finkelstein on small polyhedra. Regular (crystalline) lattices, such as close-packed hexagonals, were found to be too limited so pseudo-latticses were investigated including those found in quasicrystals and the Bernal tetrahedron-based lattice that he used to represent liquid water. The Bernal lattice was considered best and used to generate model protein structures. These were much more numerous than those seen in Nature, posing the open question of why this might be.

Keywords: protein fold-space; protein structure comparison; secondary structure lattice.

Figure 1

Efimov’s tree for some beta/alpha proteins. From a small nucleus (bottom), known structures were generated by the progressive addition of secondary structure elements.

Figure 2

Protein fold-space projections. The distances among known structures are visualised by projection into Euclidean space. The structures (dots) are coloured according to structural class: red = alpha, yellow = beta, blue = alpha/beta and purple = alpha+beta. (The latter being a smaller less well-defined class). (a) As seen by Orengo et al. (1993) [14] and (b) as seen by Hou et al. (2003) [16]. Note the overall structure has remained unchanged over ten years.

Figure 3

Topology diagram and string. The encoding of a topology diagram into a string is described in the text. In the diagram, helices are circles and strands are triangles. The three secondary structure layers (alpha/beta/alpha) are encoded as A/B/C in the string and secondary structure elements (SSEs) are numbered left to right in each layer.

Figure 4

Fold dendrograms for alpha/beta proteins. (a) Calculated automatically by finding the largest common substring between topology strings which is compared in part (b) with Efimov’s “hand-made’” tree (based on a diagram similar to Figure 1). The 16 known structures used in the calculation are named and numbered while the “ancestral” structure nodes are just labelled as “number X”.

Figure 5

Stick Forms: The “stick” figures derived from a three-layer 3-6-3 (left) and a four-layer 2-4+4-2 (right) Form are shown with strands as green “sticks” and helices as thicker red “sticks”.

Figure 6

A fragment of fold space: (a) The model folds generated from the secondary structure sequence for a small protein is shown with each structure represented as a dot in a projected space (as in Figure 2). The known family from which the SSE sequence was taken is coloured red, and the model structures that correspond to other known folds are coloured green. The size of the coloured spheres is proportional to the number of family members. (b) The greater number of novel folds (white) has been likened to the preponderance of dark matter in the Universe.

Figure 7

Murzin–Finkelstein polyhedra. (a) and (b) show how the helices in two all-alpha proteins can be mapped to edges of the solids. (c) The set of polyhedra supporting three up to six helices. Including the tetrahedron, which supports two helices (not shown), three of the polyhedra are Platonic solids.

Figure 8

A Bernal lattice: (a) J. D. Bernal in the 1960s working on his model for liquid water based on tetrahedral “packing”. Since tetrahedra cannot tile space, this is a pseudo-lattice incorporating many discontinuities (hence the liquid nature of water). (b) A more recent computer-generated version (made with a program written by the author).

Figure 9

An augmented Bernal lattice: (a) a fragment of a Bernal lattice (large dots) is augmented with an additional pair of points along each edge (small dots). Vertices are selected (coloured) to represent the path of a protein chain (b) with helices on lattice edges and strands along lines connecting satellite points. Cα atom positions are marked by small spheres which are linked by a fine line. Points are coloured blue to red following the chain from its amino to carboxy terminus.

Figure 10

Model folds: A small sample of model folds is shown as a Cα backbone trace (as in Figure 9b) with the chain coloured blue to red corresponding to amino to carboxy terminus. Residues in secondary structures are marked as a small sphere. The order of the strands in the sheet is shown below each fold. Note that even though folds (a) and (d) have the same strand order, the strand direction is not recorded and these models have different folds.

Figure 11

TIM in a triacontahedron: the beta/alpha barrel structure of triosephosphate isomerase (PDB:1timA) is mapped into the core of a triacontahedron. Although the SSEs are in roughly the right positions, their relative angles are not ideal. The parts comprise a “cross-eyed” stereo pair.