Are Urban-Canopy Velocity Profiles Exponential?

Abstract

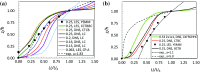
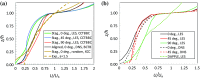
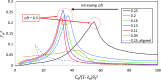
Using analyses of data from extant direct numerical simulations and large-eddy simulations of boundary-layer and channel flows over and within urban-type canopies, sectional drag forces, Reynolds and dispersive shear stresses are examined for a range of roughness densities. Using the spatially-averaged mean velocity profiles these quantities allow deduction of the canopy mixing length and sectional drag coefficient. It is shown that the common assumptions about the behaviour of these quantities, needed to produce an analytical model for the canopy velocity profile, are usually invalid, in contrast to what is found in typical vegetative (e.g. forest) canopies. The consequence is that an exponential shape of the spatially-averaged mean velocity profile within the canopy cannot normally be expected, as indeed the data demonstrate. Nonetheless, recent canopy models that allow prediction of the roughness length appropriate for the inertial layer's logarithmic profile above the canopy do not seem to depend crucially on their (invalid) assumption of an exponential profile within the canopy.

Keywords: Canopy flows; Urban environment; Velocity profiles.

Fig. 1

On left plan view of a typical cube array—a staggered array with ${\mathit{\lambda }}_p=0.11$ (Leonardi and Castro 2010). Aligned arrays would, for ${\mathit{\lambda }}_p=0.25$ for example, have cubes in boxes 1, 3, 5 $\dots$ (or 2, 4, 6, $\dots$ ) along alternate rows in the figure. At right plan view of DIPLOS array of $h\times 2h\times h$ cuboids (Castro et al. 2016)

Fig. 2

Canopy spatially-averaged mean velocity profiles for cases of flow-aligned arrays. Values of ${\mathit{\lambda }}_p$ are given in the legends. a Staggered array; b aligned array. The legends indicate data sources: YSMM (black circles), Yang et al. (2016); CCTBBC (green), Claus et al. (2012); CTCB (brown), Coceal et al. (2006); LC (black, blue, red, purple), Leonardi and Castro (2010); CXFRCHHC (green), Castro et al. (2016); BCTB (black), Branford et al. (2011); CP-A (green), Cheng and Porte-Agel (2016)

Fig. 3

Canopy spatially-averaged mean velocity profiles for ${\mathit{\lambda }}_p=0.25$. a Staggered and aligned arrays, various wind directions; CCTBBC (green), Claus et al. (2012); BCTB (black), Branford et al. (2011). The dashed line is exponential with $a=1.5$, fitting the profile for the case of staggered blocks of random height, Xie et al. (2008) (XCC, brown), which is plotted using $h=h_m$ and $U/U_h=U/U_{h_m}$. b The DIPLOS array at various wind angles, from Castro et al. (2016), and the DAPPLE array, from Xie and Castro (2009) (${\mathit{\lambda }}_p=0.53$), with a flow angle of about ${51}^{\circ }$ to the major street direction. This case was not modelled as a channel flow and thus required appropriate turbulent boundary-layer inlet conditions, as explained by Xie and Castro (2009)

Fig. 4

a Sectional drag coefficient within the canopy. All data for a staggered array of cubes with the ${\mathit{\lambda }}_p$ values given in the legend, from Leonardi and Castro (2010), except for the aligned array data from Branford et al. (2011) (BCTB, blue dashed) and the random height array of Xie et al. (2008) (XCC, brown dashed). The solid circles are experimental values obtaining during the course of the laboratory study of Cheng and Castro (2002). b Canopy mixing length, normalized (like z) by h. Legend as for a. Results from DAPPLE (Xie and Castro 2009) are included (green dashed)

Fig. 5

$l_m^2$ versus $c_d/{\mathit{\lambda }}_f^2$ for the LC data, with ${\mathit{\lambda }}_p$ values given in the right window. Data for the aligned array (BCTB, dashed lines) are included. Note the direction of increasing z and that the peak mixing length often occurs around mid-canopy height (as evident in Fig. 4b) (Recall that for cube arrays, ${\mathit{\lambda }}_p={\mathit{\lambda }}_f$.)

Fig. 6

a Reynolds shear stress ($-\overline{uw}$) in the canopy. The legend gives values of ${\mathit{\lambda }}_p$, the horizontal dashed line denotes the canopy top. The dotted lines are the expected normalised total stress—i.e. all stress components including the pressure contribution across the obstacles—(running from (1,0) to (0,8) for the domain with height 8h and (1,0) to (0,12) for the domain with height $12h$). Data are from Leonardi and Castro (2010) and (for the ${\mathit{\lambda }}_p=0.33$ cases, dashed lines) Castro et al. (2016). b The ratio of dispersive ($-\tilde{u}\tilde{w}$) to Reynolds ($-\overline{uw}$) shear stresses

Fig. 7

Mixing length profiles. Data from Leonardi and Castro (2010) cases (solid lines). In a, dashed blue line is aligned array data from Branford et al. (2011) (BCTB) and dotted line is the Coceal et al. (2006) model (CB); b includes data from Cheng and Porte-Agel (2015) (CP-A, staggered cubes in a boundary layer, long-dashed yellow and red), Branford et al. (2011) (BCTB, aligned array, long-dashed blue), Castro et al. (2016) (CXFRCHHC, aligned $1h\times 2h\times 1h$ blocks, short-dashed green and red) and random height array, Xie et al. (2008) (XCC, long-dashed brown). Figures in legends give ${\mathit{\lambda }}_p$ values

Fig. 8

Variations of $u_{\mathit{\tau }}/U_h$ and d / h (a) and $z_o/h$ (b) with wind direction. The lines are from the model of Yang et al. (2016) and the symbols are from the LES of Claus et al. (2012), both for a staggered cube array roughness with ${\mathit{\lambda }}_f=0.25$