Harnessing transition waves to realize deployable structures

Abstract

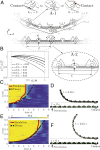
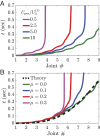
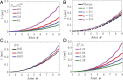
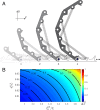
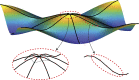
Transition waves that sequentially switch bistable elements from one stable configuration to another have received significant interest in recent years not only because of their rich physics but also, for their potential applications, including unidirectional propagation, energy harvesting, and mechanical computation. Here, we exploit the propagation of transition waves in a bistable one-dimensional (1D) linkage as a robust mechanism to realize structures that can be quickly deployed. We first use a combination of experiments and analyses to show that, if the bistable joints are properly designed, transition waves can propagate throughout the entire structure and transform the initial straight configuration into a curved one. We then demonstrate that such bistable linkages can be used as building blocks to realize deployable three-dimensional (3D) structures of arbitrary shape.

Keywords: bistable mechanism; deployable structures; multistability; transition wave.

Fig. 1.

Bistable linkage with nearest neighbor connections. (A) Schematic of the system. Insets show (A-1) the design of the joints to allow rotation in the range $\left[0,\hspace{0.17em}\mathrm{\Theta }\right]$ (note that the edges in contact are highlighted in red) and (A-2) the distance $d$. (B) Evolution of the potential energy $U_i^{\left(1\right)}$ of a joint as a function of its angle ${\theta }_i$ for various values of $d/L$. (C and E) The normalized angle of the individual bistable joints ($\theta$ for each of the joints in the linkage) during the propagation of the transition wave in a linkage with $d/L=0.02$ as recorded in two experiments in which the impactor prescribes a perturbation to the first bar characterized by $U_{\mathrm{p}\mathrm{e}\mathrm{r}}/U_0^{\left(1\right)}$ = (C) 0.50 and (E) 2.76. The corresponding numerical and theoretical predictions for the wave front are shown with solid red and dashed black lines, respectively. (D and F) Corresponding experimental snapshot of the structure in the initial (straight) and final (curved) configurations.

Fig. 2.

Effect of input energy and dissipation on the wave front. (A and B) Numerically predicted time at which each joint along the linkage with nearest neighbor connections and $d/L=0.02$ snaps for (A) different energy inputs $U_{\mathrm{p}\mathrm{e}\mathrm{r}}/U_0^{\left(1\right)}$ and (B) different friction coefficients $\mu$. Both an increase in input energy and a decrease in friction make the wave propagate further into the structure.

Fig. 3.

Bistable linkage with next-nearest neighbor connections. (A) Schematic of the system. (B) Evolution of the potential energy $U_i^{\left(2\right)}$ of a joint as a function of its angle ${\theta }_I$ for ${\theta }_{i-1}=0$ (solid line) and ${\theta }_{i-1}=\mathrm{\Theta }$ (dashed line). In both cases, ${\theta }_{i+1}=0$ and $d/L=0.02$. (C) The normalized angle of the individual bistable joints ($\theta$ for each of the joints in the linkage) during the propagation of the transition wave in a linkage with $d/L=0.02$ as recorded in an experiment in which the impactor prescribes a perturbation to the first bar characterized by $U_{\mathrm{p}\mathrm{e}\mathrm{r}}/U_0^{\left(2\right)}=0.47$. The corresponding numerical and theoretical predictions for the wave front are shown with solid red and dashed black lines, respectively. (D) Corresponding experimental snapshot of the structure in the initial (straight) and final (curved) configurations.

Fig. 4.

Effect of input energy, dissipation, and geometric parameters on the wave front. Numerically predicted time at which each joint along the linkage with next-nearest neighbor connections snaps for different (A) $U_{\mathrm{p}\mathrm{e}\mathrm{r}}/U_0^{\left(2\right)}$, (B) $\mu$, (C) $d/L$, and (D) $l_0^{\left(2\right)}/L$. In all analyses, $d/L=0.02$ unless stated otherwise.

Fig. 5.

Theoretical model. (A) Schematic of a bistable linkage with next-nearest neighbor connections as the transition wave passes through. (B) Theoretically predicted evolution of the time that it takes for the transition wave to reach the last joint, $\mathrm{\Delta }T$, as a function of the geometrical parameters $d/L$ and $l_0^{\left(2\right)}/L$.

Fig. 6.

Arbitrary surfaces can be realized by connecting our bistable linkages with next-nearest connections.

Fig. 7.

Inflection point. (A) A profile with an inflection point can be obtained by connecting two linkages with next-nearest connections. The joints at which the two linkages are connected together are shown with red circles. (B) Experimental snapshot of a structure in the initial and final configurations. Each linkage consists of four bars with $\mathrm{\Theta }=\pi /10$ and $d/L=0.02$.

Fig. 8.

The 3D deployable structures. A four-linkage structure transforms into a 3D dome-like shape. The four linkages are attached to a central rigid element (highlighted in red in Inset) and interconnected with linear springs.