Small-worldness favours network inference in synthetic neural networks

Abstract

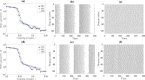
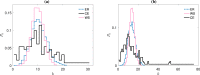
A main goal in the analysis of a complex system is to infer its underlying network structure from time-series observations of its behaviour. The inference process is often done by using bi-variate similarity measures, such as the cross-correlation (CC) or mutual information (MI), however, the main factors favouring or hindering its success are still puzzling. Here, we use synthetic neuron models in order to reveal the main topological properties that frustrate or facilitate inferring the underlying network from CC measurements. Specifically, we use pulse-coupled Izhikevich neurons connected as in the Caenorhabditis elegans neural networks as well as in networks with similar randomness and small-worldness. We analyse the effectiveness and robustness of the inference process under different observations and collective dynamics, contrasting the results obtained from using membrane potentials and inter-spike interval time-series. We find that overall, small-worldness favours network inference and degree heterogeneity hinders it. In particular, success rates in C. elegans networks - that combine small-world properties with degree heterogeneity - are closer to success rates in Erdös-Rényi network models rather than those in Watts-Strogatz network models. These results are relevant to understand better the relationship between topological properties and function in different neural networks.

Figure 1

Network inference success rates for different networks, coupling strengths, sizes and similarity measures. Panels (a,c) [Panels (b,d)] show the true positive rates, TPR, obtained using, respectively, cross correlation (CC) and mutual information (MI) measures to infer the networks connecting N = 131 [N = 277] pulse-coupled Izhikevich maps; map parameters are set such that their isolated dynamics is bursting (see Methods). The underlying connectivity structures correspond to Erdös-Rényi (ER), Watts-Strogatz (WS), or C. elegans (CE) frontal [global] neural networks. The TPR values for the ER and WS are ensemble –and initial-condition– averaged. Each of the 20 realisation with similar topological properties to that of the CE is repeated for 10 initial conditions. For the CE, the results are averaged only on the initial conditions. The TPR is found by comparing the true underlying network with the binary matrix obtained from the membrane potential time-series’ CC or MI ($T=5\times {10}^4$ iterations) after fixing a threshold such that the inferred density of connections ${\rho }_f$ matches that of the CE: ${\rho }_f\simeq 0.08$ in the left panels and ${\rho }_f\simeq 0.05$ in the right panels. The horizontal dashed line in all panels is the random inference TPR, namely, the null hypothesis.

Figure 2

Network inference success rates as a function of coupling strength and small-worldness coefficient. Using map and network parameters set as in Fig. 1, panels (a,b) [panels (c,d)] show the ensemble and initial-condition averaged TPR as function of $\epsilon$ for N = 131 [N = 277] pulse-coupled Izhikevich maps in Erdös-Rényi (ER) and Watts-Strogatz (WS) network ensembles, respectively. A successive rewiring process is done to each network realisation in order to change its small-worldness coefficient, $\sigma$, whilst maintaining the underlying density of connections and degree distribution invariant. The colour code indicates the resultant $\sigma$ for each rewiring step that increases [panels (a,c)] or decreases [panels (b,d)] the networks’ small-worldness.

Figure 3

Collective dynamics for different coupling strengths and network structures. In panel (a) we show the ensemble-averaged order parameter, R, for the inter-spike intervals time-series of N = 131 maps connected using the C. elegans frontal neural network (CE, with small-worldness coefficient $\sigma =2.8$), Erdös-Rényi (ER, with $\sigma =1.0$) and Watts-Strogatz (WS, with $\sigma =2.8$) ensembles. For the ER networks, panels (b) (ε = 0.23) and (c) (ε = 0.26) show raster plots indicating the firing pattern of the coupled neuron maps before and after the abrupt drop in panel (a)’s R values. Panel (d) shows R for the rewired ER and WS networks, such that all these ensembles have $\sigma =2.1$ (for comparison, black dots show R for the CE network also shown in panel (a)). Panels (e) (ε = 0.23) and (f) ($\epsilon =0.26$) show the corresponding raster plots.

Figure 4

Average degree distributions of our neural network structures. Panel (a) [(b)] shows the N = 131 [N = 277] nodes degree-distributions for Erdös-Rényi (ER, dashed – blue online) and Watts-Strogatz (WS, continuous – pink online) ensembles, averaged over 20 network realisations. Also, the C. elegans (CE) frontal [global] neural network structure is shown with continuous black lines.