Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2019 Dec;7(23):796.
doi: 10.21037/atm.2019.08.63.

In-depth mining of clinical data: the construction of clinical prediction model with R

Zhi-Rui Zhou  1 , Wei-Wei Wang  2 , Yan Li  3 , Kai-Rui Jin  4 , Xuan-Yi Wang  4 , Zi-Wei Wang  5 , Yi-Shan Chen  6 , Shao-Jia Wang  7 , Jing Hu  6 , Hui-Na Zhang  6 , Po Huang  6 , Guo-Zhen Zhao  6 , Xing-Xing Chen  4 , Bo Li  6 , Tian-Song Zhang  8
Affiliations

In-depth mining of clinical data: the construction of clinical prediction model with R

Zhi-Rui Zhou et al. Ann Transl Med. 2019 Dec.

Abstract

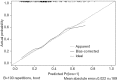
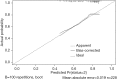
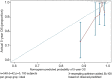
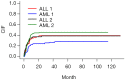
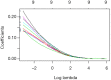
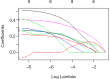
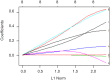
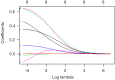
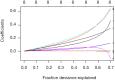
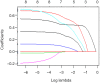
This article is the series of methodology of clinical prediction model construction (total 16 sections of this methodology series). The first section mainly introduces the concept, current application status, construction methods and processes, classification of clinical prediction models, and the necessary conditions for conducting such researches and the problems currently faced. The second episode of these series mainly concentrates on the screening method in multivariate regression analysis. The third section mainly introduces the construction method of prediction models based on Logistic regression and Nomogram drawing. The fourth episode mainly concentrates on Cox proportional hazards regression model and Nomogram drawing. The fifth Section of the series mainly introduces the calculation method of C-Statistics in the logistic regression model. The sixth section mainly introduces two common calculation methods for C-Index in Cox regression based on R. The seventh section focuses on the principle and calculation methods of Net Reclassification Index (NRI) using R. The eighth section focuses on the principle and calculation methods of IDI (Integrated Discrimination Index) using R. The ninth section continues to explore the evaluation method of clinical utility after predictive model construction: Decision Curve Analysis. The tenth section is a supplement to the previous section and mainly introduces the Decision Curve Analysis of survival outcome data. The eleventh section mainly discusses the external validation method of Logistic regression model. The twelfth mainly discusses the in-depth evaluation of Cox regression model based on R, including calculating the concordance index of discrimination (C-index) in the validation data set and drawing the calibration curve. The thirteenth section mainly introduces how to deal with the survival data outcome using competitive risk model with R. The fourteenth section mainly introduces how to draw the nomogram of the competitive risk model with R. The fifteenth section of the series mainly discusses the identification of outliers and the interpolation of missing values. The sixteenth section of the series mainly introduced the advanced variable selection methods in linear model, such as Ridge regression and LASSO regression.

Keywords: Clinical prediction models; R; statistical computing.

PubMed Disclaimer

Conflict of interest statement

Conflicts of Interest: The authors have no conflicts of interest to declare.

Figures

Figure 1
Figure 1
The flow chart of construction and evaluation of clinical prediction models.
Figure 2
Figure 2
Research process and technical routes of three prediction models.
Figure 3
Figure 3
Nomogram based on model “fit1”.
Figure 4
Figure 4
Calibration curve based on model “fit1”.
Figure 5
Figure 5
Nomogram based on model “fit2”.
Figure 6
Figure 6
Calibration curve based on model “fit2”.
Figure 7
Figure 7
Nomogram based on model “fit”.
Figure 8
Figure 8
Calibration curve based on model “fit”.
Figure 9
Figure 9
Nomogram of Cox regression model.
Figure 10
Figure 10
Calibration curve of Cox model.
Figure 11
Figure 11
Nomogram based on median survival time of Cox regression.
Figure 12
Figure 12
Nomogram based on survival probality of Cox regression model.
Figure 13
Figure 13
Calibration curve based on Cox regression model.
Figure 14
Figure 14
ROC curve.
Figure 15
Figure 15
The comparison of two models.
Figure 16
Figure 16
DCA curve.
Figure 17
Figure 17
Clinical impact curve of simple model.
Figure 18
Figure 18
Clinical impact curve of complex model.
Figure 19
Figure 19
DCA of survival outcome data.
Figure 20
Figure 20
DCA curve of “coxmod” based on Cox regression model.
Figure 21
Figure 21
DCA curves of “coxmod1” and “coxmod1” based on two Cox regression models.
Figure 22
Figure 22
DCA curve of a single predictor “thickness” based on univariate Cox regression model.
Figure 23
Figure 23
DCA curve of a single predictor “thickness” based on univariate Cox regression model. Y axis represent net reduction in interventions per 100 persons.
Figure 24
Figure 24
Calibration plot.
Figure 25
Figure 25
ROC curve.
Figure 26
Figure 26
ROC curve in validation set.
Figure 27
Figure 27
The discrimination index of Cox (2 variables) compared with Cox (5 variables) without cross-validation.
Figure 28
Figure 28
The discriminability of Cox (2 variables) compared with Cox (5 variables) with cross-validation.
Figure 29
Figure 29
The Calibration Plot performed by pec package.
Figure 30
Figure 30
The Calibration Plot performed by pec package with cross-validation.
Figure 31
Figure 31
The survival curve of cumulative recurrence rate and cumulative competitive risk event incidence rate.
Figure 32
Figure 32
Nomogram predicting cumulative recurrence risk at 36 and 60 months using the competitive risk model. Nomogram estimates that patient no. 31 has a cumulative risk of recurrence of 0.196 and 0.213 at 36 and 60 months, respectively. *, P<0.05; ***, P<0.001.
Figure 33
Figure 33
Nomogram predicting cumulative risk of recurrence at 36 and 60 months using Cox proportional hazard model. According to Nomogram’s estimate, the cumulative risk of recurrence in patient no. 31 at 36 and 60 months is 0.205 and 0.217, respectively. *, P<0.05; ***, P<0.001.
Figure 34
Figure 34
Visualization of missing values (1).
Figure 35
Figure 35
Visualization of missing values (2).
Figure 36
Figure 36
Distribution of missing values with averages.
Figure 37
Figure 37
The relationship between the coefficient and the Log(λ).
Figure 38
Figure 38
The performance of this model on the test set.
Figure 39
Figure 39
The relationship between the coefficient and the Log(λ).
Figure 40
Figure 40
The performance of this model on the test set.
Figure 41
Figure 41
Relationship between AUC and Log(λ).
Figure 42
Figure 42
The performance of this model on the test set.
Figure 43
Figure 43
The relationship between the coefficient and the L1 norm.
Figure 44
Figure 44
The relationship between the coefficient and the Log(λ).
Figure 45
Figure 45
The relationship between the coefficient and the fraction deviance explained.
Figure 46
Figure 46
The relationship between predicted and actual values in the ridge regression.
Figure 47
Figure 47
The relationship between the coefficient and the Log(λ) in the Lasso regression.
Figure 48
Figure 48
The relationship between predicted and actual values in the LASSO regression.
Figure 49
Figure 49
The relationship between the logarithm of λ and the mean square error in the LASSO regression.
See this image and copyright information in PMC

Comment in

References

    1. Reza Soroushmehr SM, Najarian K. Transforming big data into computational models for personalized medicine and health care. Dialogues Clin Neurosci 2016;18:339-43. - PMC - PubMed
    1. Bibault JE, Giraud P, Burgun A. Big Data and machine learning in radiation oncology: State of the art and future prospects. Cancer Lett 2016;382:110-7. 10.1016/j.canlet.2016.05.033 - DOI - PubMed
    1. Collins GS, Reitsma JB, Altman DG, et al. Transparent reporting of a multivariable prediction model for individual prognosis or diagnosis (TRIPOD): the TRIPOD statement. The TRIPOD Group. Circulation 2015;131:211-9. 10.1161/CIRCULATIONAHA.114.014508 - DOI - PMC - PubMed
    1. Adams ST, Leveson SH. Clinical prediction rules. Bmj 2012;344:d8312. 10.1136/bmj.d8312 - DOI - PubMed
    1. Ranstam J, Cook JA, Collins GS. Clinical prediction models. Br J Surg 2016;103:1886. 10.1002/bjs.10242 - DOI - PubMed